Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có \(\widehat {BAD} = 60^\circ \) và \(SA = SB = SD = \frac{{a\sqrt 3 }}{2}\).
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).
c) Chứng minh SB vuông góc với BC.
d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ.
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có \(\widehat {BAD} = 60^\circ \) và \(SA = SB = SD = \frac{{a\sqrt 3 }}{2}\).
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).
c) Chứng minh SB vuông góc với BC.
d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
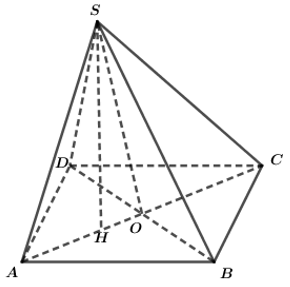
a) Tam giác ABD có: AB = AD (do ABCD là hình thoi) và \[\widehat {BAD} = 60^\circ \] (giả thiết).
Suy ra tam giác ABD đều.
Lại có SA = SB = SD = a.
Suy ra hình chóp S.ABD là hình chóp đều.
Gọi H là tâm đường tròn ngoại tiếp tam giác ABD.
Suy ra SH ⊥ (ABD).
Gọi O là giao điểm của AC và BD.
Khi đó \(AO = \frac{{AD\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\) và \(AH = \frac{2}{3}AO = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\).
Tam giác SHA vuông tại H, có: \(SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt {15} }}{6}\).
Do đó d(S, (ABCD)) = SH = \(\frac{{a\sqrt {15} }}{6}\).
Ta có \(CH = CO + OH = AO + \frac{1}{3}AO = \frac{4}{3}AO = \frac{4}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{2a\sqrt 3 }}{3}\).
Tam giác SHC vuông tại H, có: \(SC = \sqrt {S{H^2} + H{C^2}} = \sqrt {{{\left( {\frac{{a\sqrt {15} }}{6}} \right)}^2} + {{\left( {\frac{{2a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt 7 }}{2}\).
Vậy d(S, (ABCD)) = \(\frac{{a\sqrt {15} }}{6}\) và \(SC = \frac{{a\sqrt 7 }}{2}\).
b) Ta có: \(\left\{ \begin{array}{l}SH \bot \left( {ABCD} \right)\\SH \subset \left( {SAC} \right)\end{array} \right. \Rightarrow \left( {SAC} \right) \bot \left( {ABCD} \right)\).
c) Ta có H là tâm đường tròn ngoại tiếp tam giác ABD.
Suy ra BH ⊥ AD.
Lại có SH ⊥ AD (vì SH ⊥ (ABD)).
Suy ra AD ⊥ (SBH).
Mà BC // AD (do ABCD là hình thoi).
Nên BC ⊥ (SBH).
Vậy BC ⊥ SB.
d) Ta có: \(\left\{ \begin{array}{l}\left( {SBD} \right) \cap \left( {ABCD} \right) = BD\\Trong\,\,\left( {SBD} \right):\,\,SO \bot BD\\Trong\,\,\left( {ABCD} \right):\,\,AO \bot BD\end{array} \right.\)
\( \Rightarrow \) Góc giữa hai mặt phẳng (SBD) và (ABCD) là \(\widehat {SOA} = \varphi \).
Tam giác SHO vuông tại H: \(\tan \varphi = \frac{{SH}}{{OH}} = \frac{{\frac{{a\sqrt {15} }}{6}}}{{\frac{1}{3}.AO}} = \frac{{\frac{{a\sqrt {15} }}{6}}}{{\frac{1}{3}.\frac{{a\sqrt 3 }}{2}}} = \sqrt 5 \).
Vậy \(\tan \varphi = \sqrt 5 \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
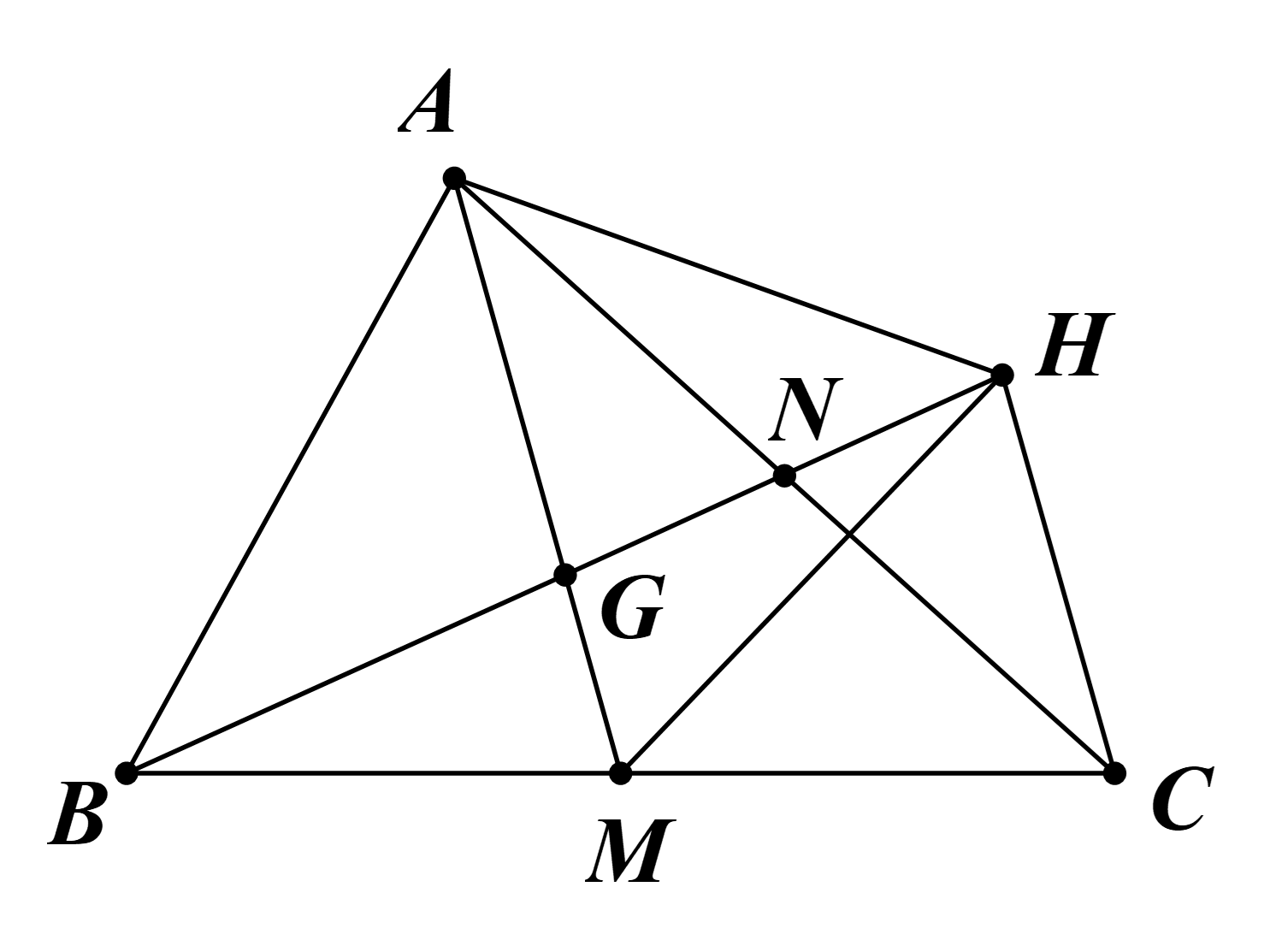
a) Gọi N là trung điểm AC.
Do H là điểm đối xứng của B qua G.
Suy ra G là trung điểm của BH.
Do đó \(GH = BG = \frac{2}{3}BN = 2GN\) (do G là trọng tâm tam giác ABC).
Vì vậy N là trung điểm GH (do 4 điểm B, G, N, H thẳng hàng).
Suy ra GN = NH.
Ta có \(\overrightarrow {AH} = \overrightarrow {AN} + \overrightarrow {NH} = \overrightarrow {AN} + \overrightarrow {GN} \)
\( = \overrightarrow {AN} + \frac{1}{3}\overrightarrow {BN} = \overrightarrow {AN} + \frac{1}{3}\left( {\overrightarrow {BA} + \overrightarrow {AN} } \right)\)
\[ = \frac{4}{3}\overrightarrow {AN} - \frac{1}{3}\overrightarrow {AB} = \frac{4}{3}\left( {\frac{1}{2}\overrightarrow {AC} } \right) - \frac{1}{3}\overrightarrow {AB} \]
\[ = \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \].
Ta có \(\overrightarrow {CH} = \overrightarrow {CN} + \overrightarrow {NH} = \overrightarrow {CN} + \overrightarrow {GN} \)
\( = \overrightarrow {CN} + \frac{1}{3}\overrightarrow {BN} = \overrightarrow {CN} + \frac{1}{3}\left( {\overrightarrow {BA} + \overrightarrow {AN} } \right)\)
\[ = \overrightarrow {CN} - \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AN} = - \frac{1}{2}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}.\frac{1}{2}\overrightarrow {AC} \]
\( = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \).
Vậy ta có điều phải chứng minh.
b) \(\overrightarrow {MH} = \overrightarrow {MB} + \overrightarrow {BH} = \frac{1}{2}\overrightarrow {CB} + \overrightarrow {BA} + \overrightarrow {AH} \)
\( = \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {AB} } \right) - \overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} \)
\( = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
Vậy ta có điều phải chứng minh.
Lời giải
Lời giải
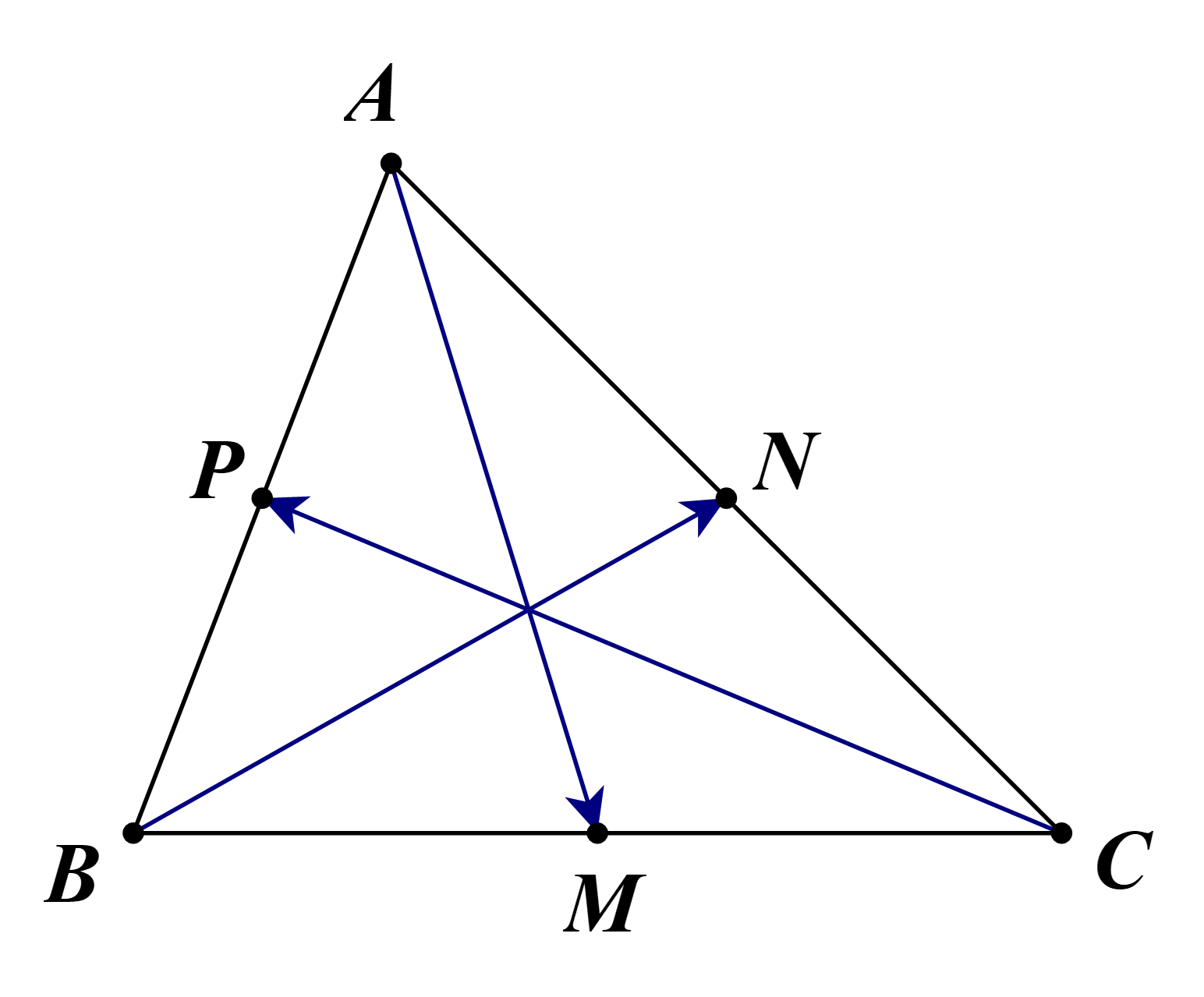
a) Ta có \(VT = \overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} \) (do M, N, P lần lượt là trung điểm của BC, CA, AB).
\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right) + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {BA} } \right) + \frac{1}{2}\left( {\overrightarrow {CB} + \overrightarrow {BC} } \right) + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {AC} } \right)\)
\( = \frac{1}{2}.\vec 0 + \frac{1}{2}.\vec 0 + \frac{1}{2}.\vec 0 = \vec 0 = VP\).
Vậy ta có điều phải chứng minh.
b) Ta có \(VT = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \frac{1}{2}\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right)\)
\( = \frac{1}{2}.2\overrightarrow {OP} + \frac{1}{2}.2\overrightarrow {ON} + \frac{1}{2}.2\overrightarrow {OM} \)
\( = \overrightarrow {OP} + \overrightarrow {ON} + \overrightarrow {OM} = VP\).
Vậy ta có điều phải chứng minh.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.