Cho tam giác nhọn ABC (AB < AC) nội tiếp trong đường tròn (O). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại M.
a) Chứng minh MA2 = MB.MC.
b) Vẽ đường cao BD của tam giác ABC. Đường thẳng qua D và song song với MA cắt AB tại E. Chứng minh tứ giác BCDE nội tiếp và xác định tâm O’ của đường tròn ngoại tiếp.
c) Tia OO’ cắt đường tròn (O) tại N. Chứng minh AN là tia phân giác của góc BAC.
d) Gọi I, K lần lượt là giao điểm của AN với BD và CE. Tìm điều kiện của tam giác ABC để có \[\frac{{IB}}{{ID}}.\frac{{KC}}{{KE}} = \frac{{IB}}{{ID}} + \frac{{KC}}{{KE}}\].
Cho tam giác nhọn ABC (AB < AC) nội tiếp trong đường tròn (O). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại M.
a) Chứng minh MA2 = MB.MC.
b) Vẽ đường cao BD của tam giác ABC. Đường thẳng qua D và song song với MA cắt AB tại E. Chứng minh tứ giác BCDE nội tiếp và xác định tâm O’ của đường tròn ngoại tiếp.
c) Tia OO’ cắt đường tròn (O) tại N. Chứng minh AN là tia phân giác của góc BAC.
d) Gọi I, K lần lượt là giao điểm của AN với BD và CE. Tìm điều kiện của tam giác ABC để có \[\frac{{IB}}{{ID}}.\frac{{KC}}{{KE}} = \frac{{IB}}{{ID}} + \frac{{KC}}{{KE}}\].
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
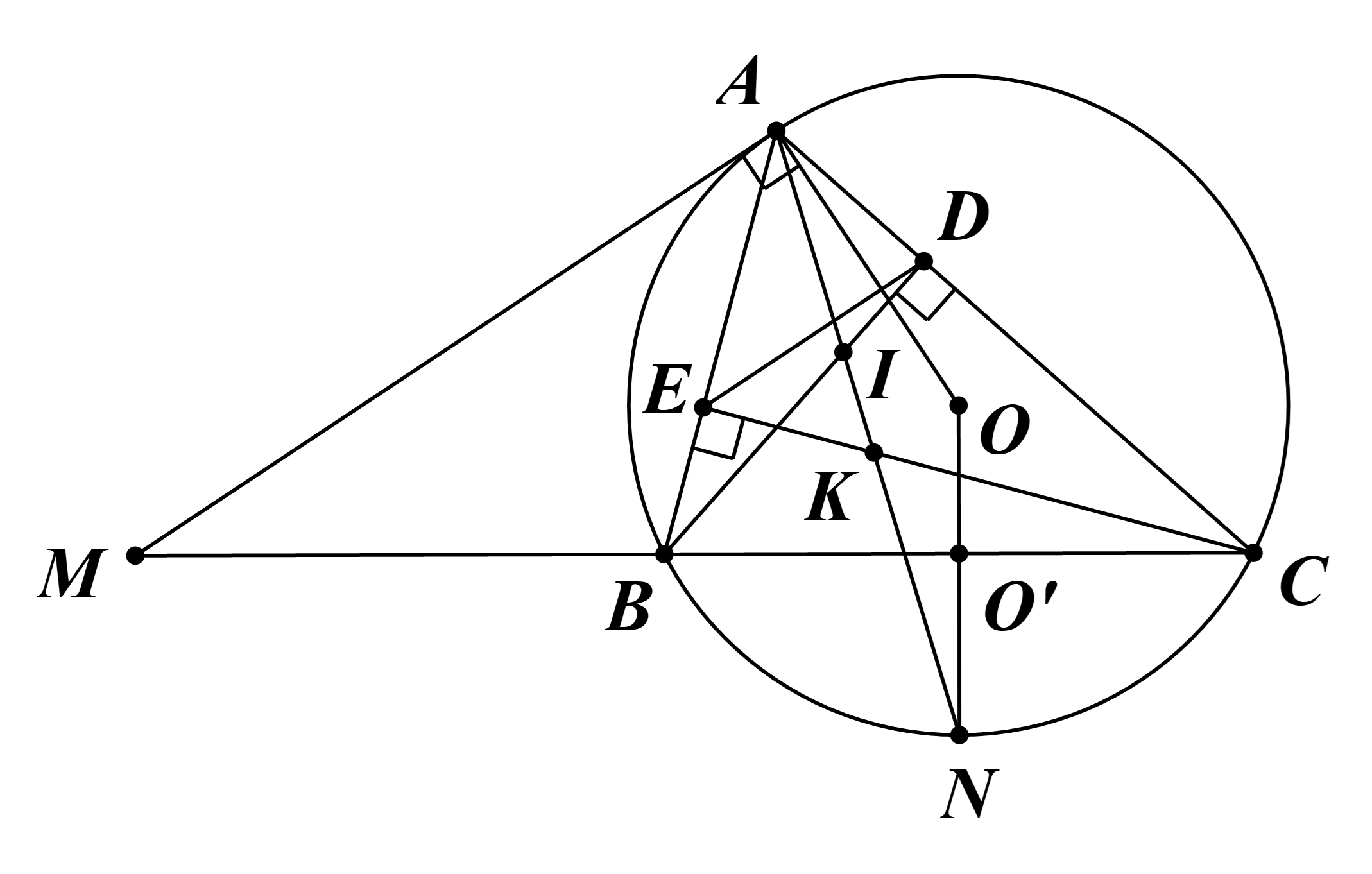
a) Xét ∆MAB và ∆MCA, có:
\[\widehat M\] chung;
\[\widehat {MAB} = \widehat {MCA}\] (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung).
Do đó (g.g).
Suy ra \[\frac{{MA}}{{MC}} = \frac{{MB}}{{MA}}\].
⇔ MA2 = MB.MC.
Vậy ta có điều phải chứng minh.
b) Ta có DE // AM (giả thiết).
Suy ra \[\widehat {MAB} = \widehat {AED}\] (cặp góc so le trong).
Mà \[\widehat {MAB} = \widehat {MCA}\] (chứng minh trên).
Do đó \[\widehat {MCA} = \widehat {AED}\].
Vì vậy tứ giác BCDE là tứ giác nội tiếp được.
Ta có \[\widehat {BEC} = \widehat {BDC} = 90^\circ \] (cùng chắn ).
Suy ra tứ giác BCDE nội tiếp đường tròn đường kính BC.
Vậy tâm O’ của đường tròn ngoại tiếp tứ giác BCDE là trung điểm cạnh BC.
c) Do O’ là trung điểm BC (chứng minh trên) và OO’ cắt (O) tại N.
Suy ra N là điểm chính giữa của .
Khi đó .
Suy ra \[\widehat {BAN} = \widehat {NAC}\].
Vậy AN là tia phân giác của \[\widehat {BAC}\].
d) Ta có AI là đường phân giác của tam giác ABD.
Suy ra \[\frac{{IB}}{{ID}} = \frac{{AB}}{{AD}}\] (tính chất đường phân giác).
Tương tự, ta có \[\frac{{KC}}{{KE}} = \frac{{AC}}{{AE}}\].
Xét ∆ABC và ∆ADE, có:
\[\widehat A\] chung;
\[\widehat {MCA} = \widehat {AED}\] (chứng minh trên).
Do đó (g.g).
Suy ra \[\frac{{AB}}{{AD}} = \frac{{AC}}{{AE}}\].
Do đó AB.AE = AC.AD.
Ta có \[\frac{{IB}}{{ID}}.\frac{{KC}}{{KE}} = \frac{{IB}}{{ID}} + \frac{{KC}}{{KE}}\].
\[ \Leftrightarrow \frac{{AB}}{{AD}}.\frac{{AC}}{{AE}} = \frac{{AB}}{{AD}} + \frac{{AC}}{{AE}}\]
\[ \Leftrightarrow \frac{{AB}}{{AD}}.\frac{{AC}}{{AE}} = \frac{{AB.AE + AC.AD}}{{AD.AE}}\]
⇔ AB.AC = AB.AE + AC.AD
\[ \Leftrightarrow AB.AC = AB.\frac{1}{2}AC + AC.\frac{1}{2}AB\].
Vì vậy để \[\frac{{IB}}{{ID}}.\frac{{KC}}{{KE}} = \frac{{IB}}{{ID}} + \frac{{KC}}{{KE}}\] thì ta cần \[AE = \frac{1}{2}AC\] và \[AD = \frac{1}{2}AB\].
Tam giác ABD vuông tại D: \[\cos \widehat {BAD} = \frac{{AD}}{{AB}} = \frac{1}{2}\].
Suy ra \[\widehat {BAD} = 60^\circ \].
Vậy tam giác ABC cần có thêm điều kiện \[\widehat {BAC} = 60^\circ \] thì ta có \[\frac{{IB}}{{ID}}.\frac{{KC}}{{KE}} = \frac{{IB}}{{ID}} + \frac{{KC}}{{KE}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Muốn đổi hỗn số thành số thập phân, ta làm các bước sau:
Bước 1: Đưa hỗn số thành phân số:
– Lấy phần nguyên nhân với mẫu số, kết quả nhận được cộng thêm tử số;
– Thay kết quả ở trên thành tử số mới, giữ nguyên mẫu số, ta được một phân số từ hỗn số đã cho.
Bước 2: Đưa mẫu số về 10; 100; 1000; … và thực hiện đổi phân số thập phân về số thập phân.
Ví dụ: Đổi các hỗn số \(5\frac{1}{{10}}\) và \(5\frac{3}{4}\) thành số thập phân.
Hướng dẫn giải
Ta có: \(5\frac{1}{{10}} = \frac{{5 \times 10 + 1}}{{10}} = \frac{{51}}{{10}} = 5,1\);
\(5\frac{3}{4} = \frac{{5 \times 4 + 3}}{4} = \frac{{23}}{4} = \frac{{23 \times 25}}{{4 \times 25}} = \frac{{575}}{{100}} = 5,75\).
Câu 2
Lời giải
Lời giải
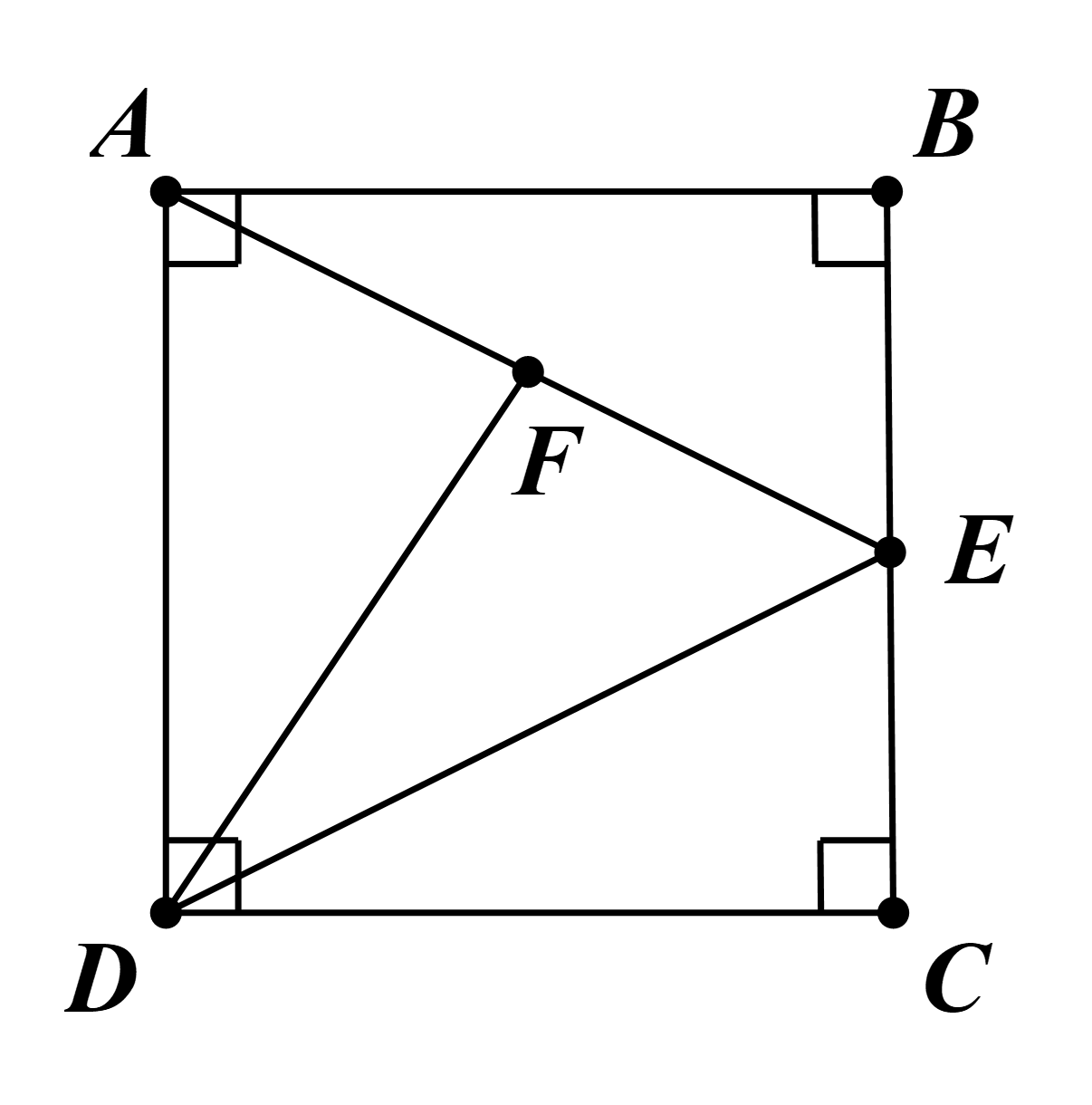
Ta có E là trung điểm BC.
Suy ra \(CE = \frac{{BC}}{2} = \frac{a}{2}\).
Ta có AB = CD (do ABCD là hình vuông) và BE = CE (E là trung điểm BC).
Suy ra \(\sqrt {A{B^2} + B{E^2}} = \sqrt {C{D^2} + C{E^2}} \).
Do đó AE = DE.
Tam giác CDE vuông tại C: \(AE = DE = \sqrt {C{D^2} + C{E^2}} = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\).
Ta có \(D{F^2} = \frac{{2D{A^2} + 2D{E^2} - A{E^2}}}{4} = \frac{{2{a^2} + 2{{\left( {\frac{{a\sqrt 5 }}{2}} \right)}^2} - {{\left( {\frac{{a\sqrt 5 }}{2}} \right)}^2}}}{4} = \frac{{13{a^2}}}{{16}}\).
Vậy \(DF = \frac{{a\sqrt {13} }}{4}\).
Do đó ta chọn phương án A.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.