Câu hỏi:

12/07/2024 342

Cho tam giác cân ABC có CA = CB và góc ABC nhọn. Các đường cao CD, BE, AF cắt nhau ở H.

a) Chứng minh 4 điểm C, F, H, E nằm trên đường tròn (O). Xác định tâm O của đường tròn.

b) Chứng minh (O) tiếp xúc với đường tròn ngoại tiếp tam giác ABC.

c) Chứng minh DF là tiếp tuyến của đường tròn (O).

d) Chứng minh FB là phân giác của góc DFE.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

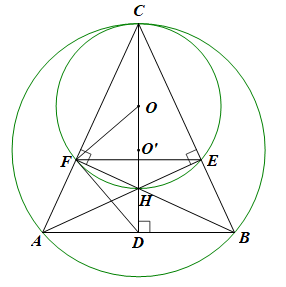
Media VietJack

a) Ta có: \(AE \bot BC,BF \bot AC\) nên \[\widehat {CFH} = \widehat {CEH} = 90^\circ \].

Do đó F, E cùng nằm trên đường tròn đường kính CH.

Suy ra 4 điểm C, F, H, E cùng nằm trên đường tròn (O) đường kính CH với O là trung điểm của CH.

b) Gọi (O’) là đường tròn ngoại tiếp tam giác ABC.

Do tam giác ABC có CA = CB nên tam giác ABC cân tại C

Do đó tâm O’ của đường tròn ngoại tiếp tam giác nằm trên đường cao CD.

Suy ra 3 điểm C, O, O’ thẳng hàng và OO’ = O’C – OC.

Lại có C cùng nằm trên đường tròn (O) và (O’)

Vậy (O) tiếp xúc với (O’) với (O’) là đường tròn ngoại tiếp tam giác ABC.

c) Chứng minh tương tự câu a ta cũng có tứ giác AFHD là tứ giác nội tiếp

Suy ra \(\widehat {HFD} = \widehat {HAD}\) (hai góc nội tiếp cùng chắn cung HD).

Lại có \(\widehat {HAD} = \widehat {ECH}\) (do cùng phụ với \(\widehat {AHD} = \widehat {CHE}\))

\(\widehat {ECH} = \widehat {FCH}\) (do tam giác ABC cân tại C nên CH là đường phân giác)

\(\widehat {FCH} = \widehat {FCO} = \widehat {CFO}\) (do tam giác OCF có OC = OF nên là tam giác cân tại O)

Do đó \(\widehat {HFD} = \widehat {CFO}\).

Mặt khác \(\widehat {CFO} + \widehat {OFH} = 90^\circ \) nên \(\widehat {HFD} + \widehat {{\rm{OF}}H} = 90^\circ \)

Hay \(\widehat {DFO} = 90^\circ \)

Mà F nằm trên (O) nên DF là tiếp tuyến của (O).

d) Do DF là tiếp tuyến của (O) nên \(\widehat {DFH} = \widehat {FCH}\) (tính chất góc tạo bởi tia tiếp tuyến và dây cung với góc nội tiếp đường tròn cùng chắn cung đó)

Ta cũng có \(\widehat {EFH} = \widehat {ECH}\) (hai góc nội tiếp cùng chắn cung EH)

Mà \(\widehat {FCH} = \widehat {ECH}\) (do CH là phân giác của góc ACB)

Suy ra \(\widehat {EFH} = \widehat {DFH}\)

Do đó FB là phân giác của \(\widehat {DFE}\).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác đều ABC cạnh a, điểm M là trung điểm BC. Dựng các vectơ sau và tính độ dài của chúng.

a) \(\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} \);

b) \(\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} \);

c) \(\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} \);

d) \(\frac{3}{4}\overrightarrow {MA} - 2,5\overrightarrow {MB} \).

Xem đáp án

Lời giải

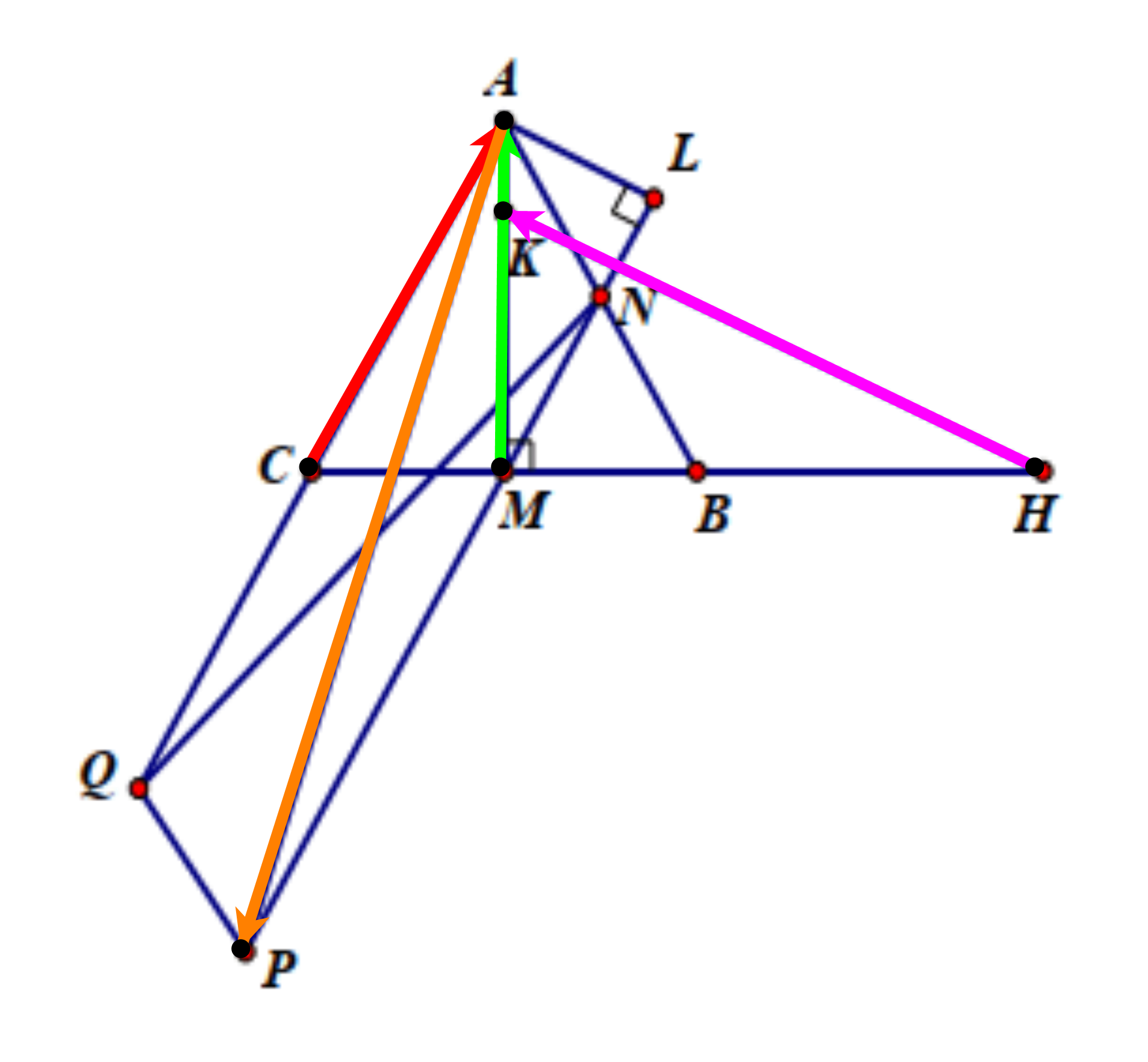
Media VietJack

a) Ta có \(\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} = \overrightarrow {CM} + \overrightarrow {MA} = \overrightarrow {CA} \) (do M là trung điểm BC).

Vậy \(\left| {\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} } \right| = \left| {\overrightarrow {CA} } \right| = CA = a\).

b) Ta có \(\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} = \overrightarrow {BA} - \overrightarrow {BM} = \overrightarrow {MA} \) (do M là trung điểm BC).

Tam giác ABC đều cạnh a có M là trung điểm BC.

Suy ra \(CM = BM = \frac{{BC}}{2} = \frac{a}{2}\).

Tam giác ABC đều có AM là đường trung tuyến.

Suy ra AM cũng là đường cao của tam giác ABC.

Tam giác ACM vuông tại M: \(AM = \sqrt {A{C^2} - C{M^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\).

Vậy \(\left| {\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} } \right| = \left| {\overrightarrow {MA} } \right| = MA = \frac{{a\sqrt 3 }}{2}\).

c) Ta có \(\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} = \overrightarrow {AN} + \overrightarrow {AQ} \), với N, C là trung điểm AB, AQ.

\( = \overrightarrow {AP} \), với P là đỉnh của hình bình hành AQPN.

Gọi L là hình chiếu của A lên PN.

Ta có MN // AC (MN là đường trung bình của ∆ABC).

Suy ra \(\widehat {ANL} = \widehat {MNB} = \widehat {ACB} = 60^\circ \).

Tam giác ANL vuông tại L:

⦁ \(\sin \widehat {ANL} = \frac{{AL}}{{AN}} \Rightarrow AL = \frac{a}{2}.\sin 60^\circ = \frac{{a\sqrt 3 }}{4}\);

⦁ \(\cos \widehat {ANL} = \frac{{NL}}{{AN}} \Rightarrow NL = \frac{a}{2}.\cos 60^\circ = \frac{a}{4}\).

Ta có PL = PN + NL = AQ + NL = 2AC + NL \( = 2a + \frac{a}{4} = \frac{{9a}}{4}\).

Tam giác ALP vuông tại L: \(AP = \sqrt {A{L^2} + P{L^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{4}} \right)}^2} + {{\left( {\frac{{9a}}{4}} \right)}^2}} = \frac{{a\sqrt {21} }}{2}\).

Vậy \(\left| {\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} } \right| = \left| {\overrightarrow {AP} } \right| = AP = \frac{{a\sqrt {21} }}{2}\).

d) Gọi K là điểm nằm trên đoạn AM thỏa mãn \(MK = \frac{3}{4}MA\)và H là điểm thuộc tia MB sao cho MH = 2,5MB.

Khi đó \(\overrightarrow {MK} = \frac{3}{4}\overrightarrow {MA} ,\,\,\overrightarrow {MH} = 2,5\overrightarrow {MB} \).

Ta có \(\frac{3}{4}\overrightarrow {MA} - 2,5\overrightarrow {MB} = \overrightarrow {MK} - \overrightarrow {MH} = \overrightarrow {HK} \).

Ta có \(MK = \frac{3}{4}MA = \frac{3}{4}.\frac{{a\sqrt 3 }}{2} = \frac{{3a\sqrt 3 }}{8}\) và \(MH = 2,5MB = 2,5.\frac{a}{2} = \frac{{5a}}{4}\).

Tam giác KMH vuông tại M: \(HK = \sqrt {M{K^2} + M{H^2}} = \sqrt {{{\left( {\frac{{3a\sqrt 3 }}{8}} \right)}^2} + {{\left( {\frac{{5a}}{4}} \right)}^2}} = \frac{{a\sqrt {127} }}{8}\).

Vậy \(\left| {\frac{3}{4}\overrightarrow {MA} - 2,5\overrightarrow {MB} } \right| = \left| {\overrightarrow {HK} } \right| = HK = \frac{{a\sqrt {127} }}{8}\).

Câu 2

Cho biểu thức \(P = \frac{{{x^2} + x}}{{{x^2} - 2x + 1}}:\left( {\frac{{x + 1}}{x} - \frac{1}{{1 - x}} + \frac{{2 - {x^2}}}{{{x^2} - x}}} \right)\).

a) Rút gọn P.

b) Tìm x để P < 1.

c) Tìm giá trị nhỏ nhất của P khi x > 2.

Xem đáp án

Lời giải

a) \(P = \frac{{{x^2} + x}}{{{x^2} - 2x + 1}}:\left( {\frac{{x + 1}}{x} - \frac{1}{{1 - x}} + \frac{{2 - {x^2}}}{{{x^2} - x}}} \right)\)

\( = \frac{{x\left( {x + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}:\left[ {\frac{{x + 1}}{x} + \frac{1}{{x - 1}} + \frac{{2 - {x^2}}}{{x\left( {x - 1} \right)}}} \right]\)

\( = \frac{{x\left( {x + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}:\left[ {\frac{{\left( {x + 1} \right)\left( {x - 1} \right) + x + 2 - {x^2}}}{{x\left( {x - 1} \right)}}} \right]\)

\( = \frac{{x\left( {x + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}:\frac{{x + 1}}{{x\left( {x - 1} \right)}} = \frac{{x\left( {x + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}.\frac{{x\left( {x - 1} \right)}}{{x + 1}} = \frac{{{x^2}}}{{x - 1}}\).

b) Ta có \(P < 1 \Leftrightarrow \frac{{{x^2}}}{{x - 1}} < 1\)

\[ \Leftrightarrow \frac{{{x^2}}}{{x - 1}} - 1 < 0 \Leftrightarrow \frac{{{x^2} - x + 1}}{{x - 1}} < 0\]

\[ \Leftrightarrow \frac{{{{\left( {x - \frac{1}{2}} \right)}^2} + \frac{3}{4}}}{{x - 1}} < 0 \Leftrightarrow x - 1 < 0\] (vì \[{\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4} \ge \frac{3}{4} > 0,\,\,\forall x \in \mathbb{R}\]).

⇔ x < 1.

Vậy x < 1 thì P < 1.

c) Vì x > 2 nên x – 2 > 0.

Do đó x – 1 > x – 2 > 0.

Ta có \(P = \frac{{{x^2}}}{{x - 1}} = \frac{{{x^2} - 1 + 1}}{{x - 1}} = x + 1 + \frac{1}{{x - 1}} = x - 1 + \frac{1}{{x - 1}} + 2\).

Áp dụng bất đẳng thức Cauchy, ta có: \(x - 1 + \frac{1}{{x - 1}} \ge 2\sqrt {\frac{{x - 1}}{{x - 1}}} = 2\sqrt 1 = 2,\,\forall x > 2\).

\( \Leftrightarrow x - 1 + \frac{1}{{x - 1}} + 2 \ge 2 + 2 = 4\).

⇔ P ≥ 4.

Dấu “=” xảy ra ⇔ (x – 1)² = 1 ⇔ x – 1 = 1 hoặc x – 1 = –1.

⇔ x = 2 (loại vì x > 2) hoặc x = 0 (loại vì x > 2).

Vậy P không có giá trị nhỏ nhất khi x > 2.

Câu 3