Cho đường tròn (O; R) và dây MN. Các tiếp tuyến của (O) tại M, N cắt nhau ở A. Qua M, kẻ đường thẳng song song với AN, cắt (O) tại điểm thứ hai là P. Q là giao điểm của AP và (O), K là giao điểm của MQ và AN. Chứng minh
a) AK2 = KQ.KM.
b) K là trung điểm của AN.
Cho đường tròn (O; R) và dây MN. Các tiếp tuyến của (O) tại M, N cắt nhau ở A. Qua M, kẻ đường thẳng song song với AN, cắt (O) tại điểm thứ hai là P. Q là giao điểm của AP và (O), K là giao điểm của MQ và AN. Chứng minh
a) AK2 = KQ.KM.
b) K là trung điểm của AN.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
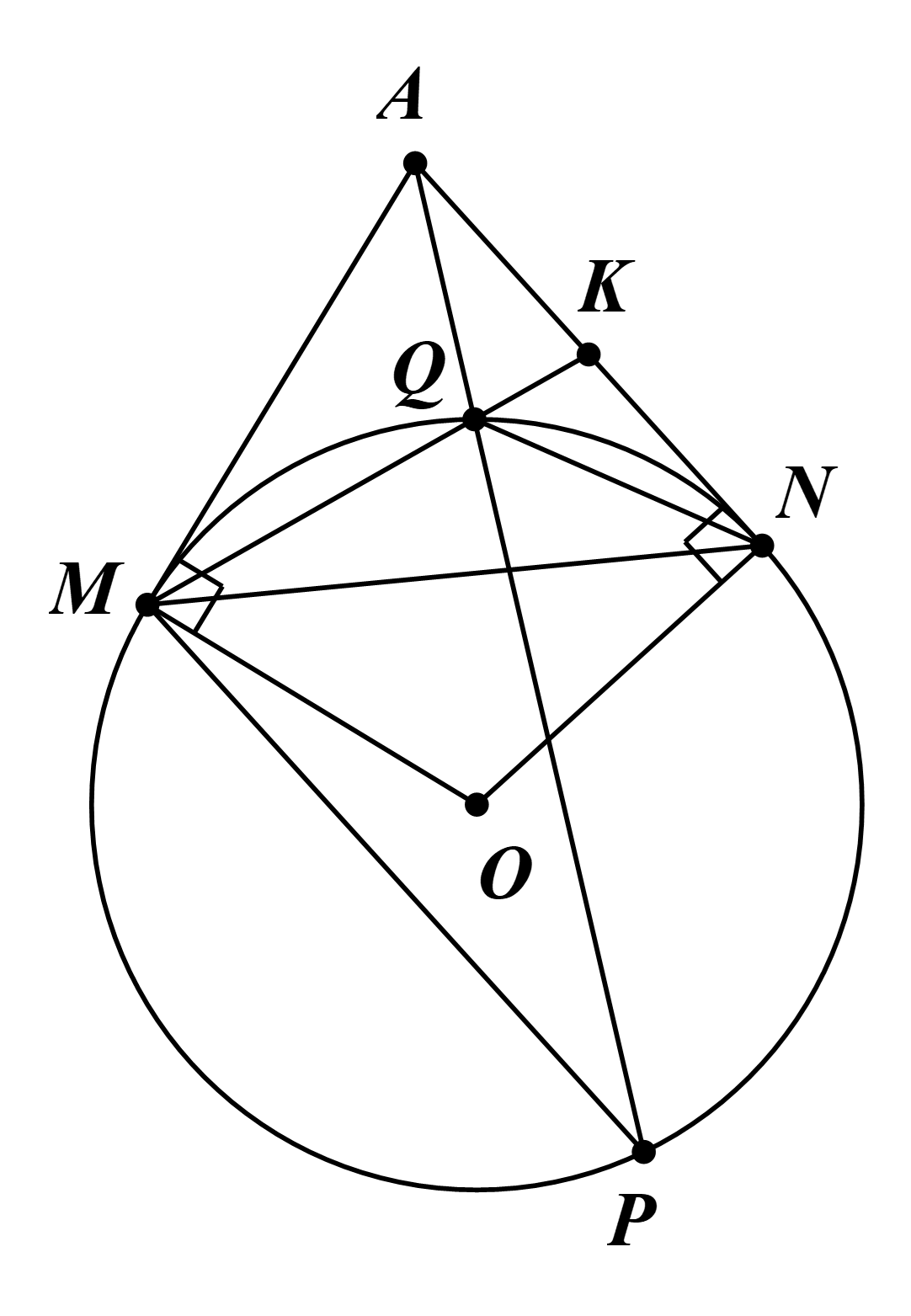
a) Ta có \(\widehat {AMQ} = \widehat {MPQ}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung) và \(\widehat {QAK} = \widehat {MPQ}\) (do AK // MP).
Suy ra \(\widehat {AMQ} = \widehat {QAK}\).
Xét ∆AKQ và ∆MAK, có:
\(\widehat {AMQ} = \widehat {QAK}\) (chứng minh trên);
\(\widehat {AKQ}\) chung.
Do đó (g.g).
Suy ra \(\frac{{AK}}{{MA}} = \frac{{KQ}}{{AK}} = \frac{{AQ}}{{MK}}\).
\[ \Leftrightarrow \frac{{AK}}{{MA}} = \frac{{MK}}{{AK}} = \frac{{AQ}}{{KQ}}\]
\[ \Leftrightarrow \frac{{AK}}{{MK}} = \frac{{MA}}{{AK}} = \frac{{AQ}}{{KQ}}\]
\[ \Leftrightarrow \frac{{AK}}{{MK}} = \frac{{KQ}}{{AK}} = \frac{{AQ}}{{MA}}\].
Vậy AK2 = KQ.KM (điều phải chứng minh).
b) Xét ∆KQN và ∆KNM, có:
\(\widehat {KNQ} = \widehat {KMN}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung);
\(\widehat {MKN}\) chung.
Do đó (g.g).
Suy ra \(\frac{{KQ}}{{KN}} = \frac{{QN}}{{NM}} = \frac{{KN}}{{KM}}\).
Do đó KN2 = KQ.KM.
Mà AK2 = KQ.KM (câu a).
Suy ra KN = AK.
Vậy K là trung điểm AN.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
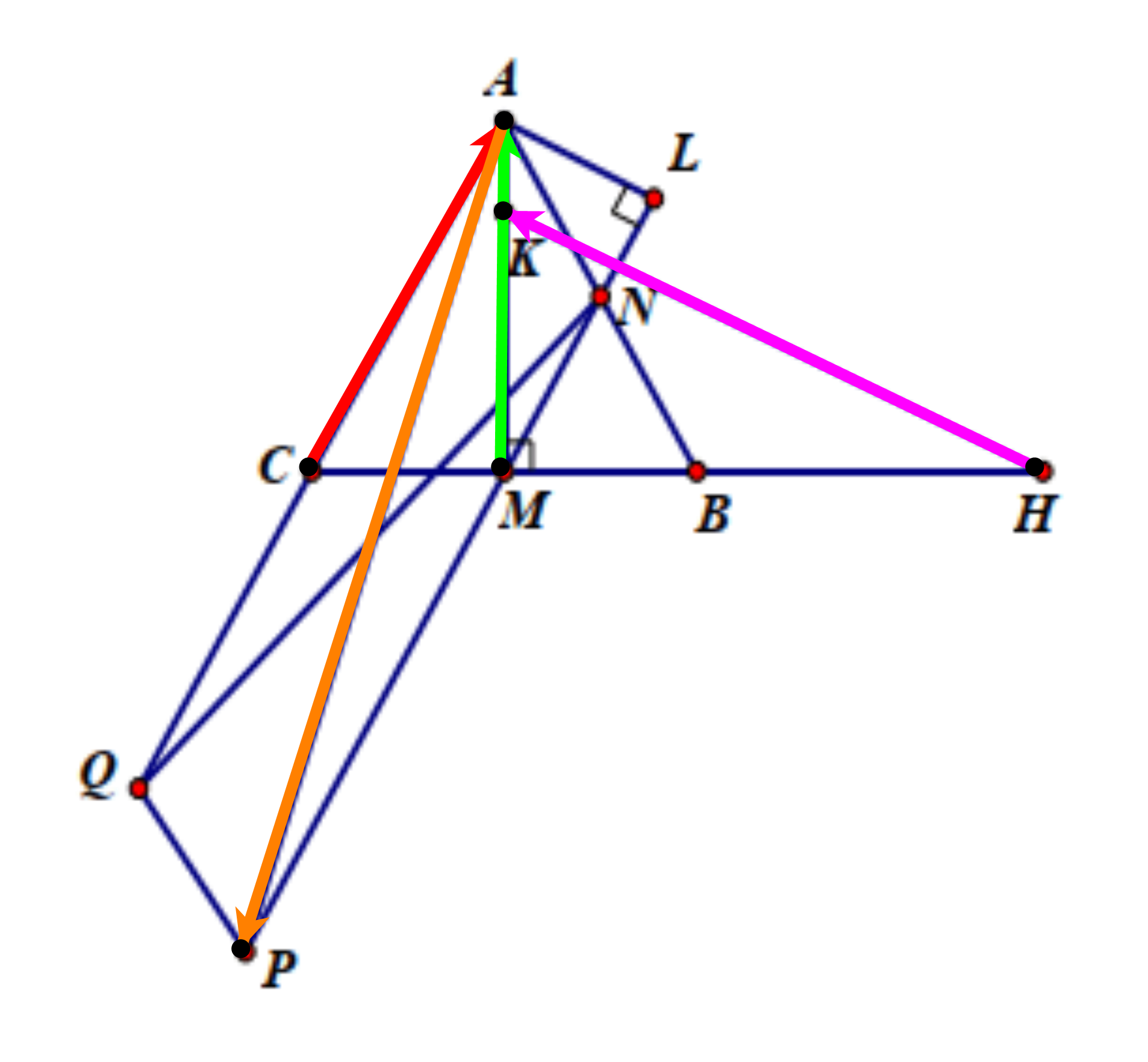
a) Ta có \(\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} = \overrightarrow {CM} + \overrightarrow {MA} = \overrightarrow {CA} \) (do M là trung điểm BC).
Vậy \(\left| {\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} } \right| = \left| {\overrightarrow {CA} } \right| = CA = a\).
b) Ta có \(\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} = \overrightarrow {BA} - \overrightarrow {BM} = \overrightarrow {MA} \) (do M là trung điểm BC).
Tam giác ABC đều cạnh a có M là trung điểm BC.
Suy ra \(CM = BM = \frac{{BC}}{2} = \frac{a}{2}\).
Tam giác ABC đều có AM là đường trung tuyến.
Suy ra AM cũng là đường cao của tam giác ABC.
Tam giác ACM vuông tại M: \(AM = \sqrt {A{C^2} - C{M^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\).
Vậy \(\left| {\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} } \right| = \left| {\overrightarrow {MA} } \right| = MA = \frac{{a\sqrt 3 }}{2}\).
c) Ta có \(\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} = \overrightarrow {AN} + \overrightarrow {AQ} \), với N, C là trung điểm AB, AQ.
\( = \overrightarrow {AP} \), với P là đỉnh của hình bình hành AQPN.
Gọi L là hình chiếu của A lên PN.
Ta có MN // AC (MN là đường trung bình của ∆ABC).
Suy ra \(\widehat {ANL} = \widehat {MNB} = \widehat {ACB} = 60^\circ \).
Tam giác ANL vuông tại L:
⦁ \(\sin \widehat {ANL} = \frac{{AL}}{{AN}} \Rightarrow AL = \frac{a}{2}.\sin 60^\circ = \frac{{a\sqrt 3 }}{4}\);
⦁ \(\cos \widehat {ANL} = \frac{{NL}}{{AN}} \Rightarrow NL = \frac{a}{2}.\cos 60^\circ = \frac{a}{4}\).
Ta có PL = PN + NL = AQ + NL = 2AC + NL \( = 2a + \frac{a}{4} = \frac{{9a}}{4}\).
Tam giác ALP vuông tại L: \(AP = \sqrt {A{L^2} + P{L^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{4}} \right)}^2} + {{\left( {\frac{{9a}}{4}} \right)}^2}} = \frac{{a\sqrt {21} }}{2}\).
Vậy \(\left| {\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} } \right| = \left| {\overrightarrow {AP} } \right| = AP = \frac{{a\sqrt {21} }}{2}\).
d) Gọi K là điểm nằm trên đoạn AM thỏa mãn \(MK = \frac{3}{4}MA\)và H là điểm thuộc tia MB sao cho MH = 2,5MB.
Khi đó \(\overrightarrow {MK} = \frac{3}{4}\overrightarrow {MA} ,\,\,\overrightarrow {MH} = 2,5\overrightarrow {MB} \).
Ta có \(\frac{3}{4}\overrightarrow {MA} - 2,5\overrightarrow {MB} = \overrightarrow {MK} - \overrightarrow {MH} = \overrightarrow {HK} \).
Ta có \(MK = \frac{3}{4}MA = \frac{3}{4}.\frac{{a\sqrt 3 }}{2} = \frac{{3a\sqrt 3 }}{8}\) và \(MH = 2,5MB = 2,5.\frac{a}{2} = \frac{{5a}}{4}\).
Tam giác KMH vuông tại M: \(HK = \sqrt {M{K^2} + M{H^2}} = \sqrt {{{\left( {\frac{{3a\sqrt 3 }}{8}} \right)}^2} + {{\left( {\frac{{5a}}{4}} \right)}^2}} = \frac{{a\sqrt {127} }}{8}\).
Vậy \(\left| {\frac{3}{4}\overrightarrow {MA} - 2,5\overrightarrow {MB} } \right| = \left| {\overrightarrow {HK} } \right| = HK = \frac{{a\sqrt {127} }}{8}\).Lời giải
Lời giải
a) \(P = \frac{{{x^2} + x}}{{{x^2} - 2x + 1}}:\left( {\frac{{x + 1}}{x} - \frac{1}{{1 - x}} + \frac{{2 - {x^2}}}{{{x^2} - x}}} \right)\)
\( = \frac{{x\left( {x + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}:\left[ {\frac{{x + 1}}{x} + \frac{1}{{x - 1}} + \frac{{2 - {x^2}}}{{x\left( {x - 1} \right)}}} \right]\)
\( = \frac{{x\left( {x + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}:\left[ {\frac{{\left( {x + 1} \right)\left( {x - 1} \right) + x + 2 - {x^2}}}{{x\left( {x - 1} \right)}}} \right]\)
\( = \frac{{x\left( {x + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}:\frac{{x + 1}}{{x\left( {x - 1} \right)}} = \frac{{x\left( {x + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}.\frac{{x\left( {x - 1} \right)}}{{x + 1}} = \frac{{{x^2}}}{{x - 1}}\).
b) Ta có \(P < 1 \Leftrightarrow \frac{{{x^2}}}{{x - 1}} < 1\)
\[ \Leftrightarrow \frac{{{x^2}}}{{x - 1}} - 1 < 0 \Leftrightarrow \frac{{{x^2} - x + 1}}{{x - 1}} < 0\]
\[ \Leftrightarrow \frac{{{{\left( {x - \frac{1}{2}} \right)}^2} + \frac{3}{4}}}{{x - 1}} < 0 \Leftrightarrow x - 1 < 0\] (vì \[{\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4} \ge \frac{3}{4} > 0,\,\,\forall x \in \mathbb{R}\]).
⇔ x < 1.
Vậy x < 1 thì P < 1.
c) Vì x > 2 nên x – 2 > 0.
Do đó x – 1 > x – 2 > 0.
Ta có \(P = \frac{{{x^2}}}{{x - 1}} = \frac{{{x^2} - 1 + 1}}{{x - 1}} = x + 1 + \frac{1}{{x - 1}} = x - 1 + \frac{1}{{x - 1}} + 2\).
Áp dụng bất đẳng thức Cauchy, ta có: \(x - 1 + \frac{1}{{x - 1}} \ge 2\sqrt {\frac{{x - 1}}{{x - 1}}} = 2\sqrt 1 = 2,\,\forall x > 2\).
\( \Leftrightarrow x - 1 + \frac{1}{{x - 1}} + 2 \ge 2 + 2 = 4\).
⇔ P ≥ 4.
Dấu “=” xảy ra ⇔ (x – 1)2 = 1 ⇔ x – 1 = 1 hoặc x – 1 = –1.
⇔ x = 2 (loại vì x > 2) hoặc x = 0 (loại vì x > 2).
Vậy P không có giá trị nhỏ nhất khi x > 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.