Cho hàm số bậc bốn f (x) có bảng biến thiên như sau:

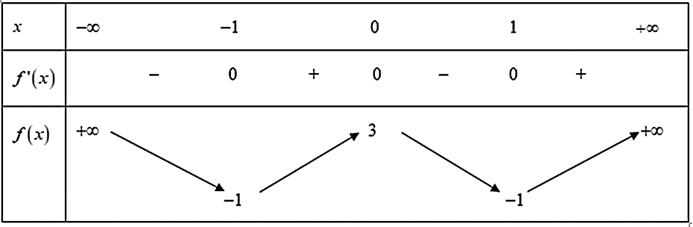
Số điểm cực trị của hàm số g(x) = x⁴[f (x − 1)]² là:

Lời giải

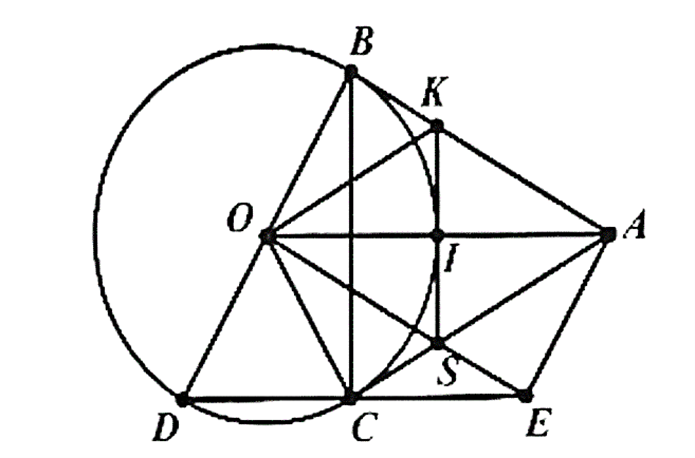
a) Ta có AB và AC là tiếp tuyến của (O) \( \Rightarrow \widehat {ABO} = \widehat {ACO} = 90^\circ \).

Xét tứ giác ABOC có:

\(\widehat {ABO} + \widehat {ACO} = 90^\circ + 90^\circ = 180^\circ \).

Suy ra tứ giác ABOC là tứ giác nội tiếp đường tròn.

Hay A, B, O, C thuộc 1 đường tròn.

b) Ta có: AB và AC là tiếp tuyến của (O) Þ AB = AC.

Mà OB = OC = R Þ OA là đường trung trực của BC hay OA ^ BC (1)

Xét ∆CBD nội tiếp (O) có BD là đường kính của (O).

Suy ra ∆CBD vuông tại C hay DC ^ BC (2)

Từ (1), (2) Þ DC // OA.

c) Ta có: DC // OA Þ CE // OA Þ OCEA là hình thang (3)

Ta có: \[\widehat {ODE} + \widehat {OBC} = 90^\circ \];

\(\widehat {OBC} + \widehat {BOA} = 90^\circ \).

Suy ra \(\widehat {ODE} = \widehat {BOA}\).

Xét ∆BOA và ∆ODE có:

\(\widehat {ODE} = \widehat {BOA}\) (cmt)

\[\widehat {DOE} = \widehat {OBA} = 90^\circ \]

OB = OD = R

Þ ∆BOA = ∆ODE (g.c.g)

Þ AB = OE (hai cạnh tương ứng)

Mà AB = AC (AB và AC đều là tiếp tuyến chung của (O))

Suy ra OE = AC (4)

Từ (3) và (4) Þ OCEA là hình thang cân.

d) Ta có: \[\widehat {SOI} + \widehat {AOB} = 90^\circ \]

\(\widehat {AOB} + \widehat {OAB} = 90^\circ \)

\(\widehat {OAB} = \widehat {SAO}\)

Suy ra \(\widehat {SOA} = \widehat {SAO}\) Þ ∆SOA cân tại S

Lại có SI là đường trung tuyến \(\left( {OI = IA = \frac{{OA}}{2} = R} \right)\)

Suy ra SI ^ OA Þ KS ^ OA (5)

Ta có ∆KAS có \(\widehat {KAI} = \widehat {SAI}\)

AI ^ KS suy ra KI = SI.

Mà OI ^ AI

Suy ra OKAS là hình bình hành (6)

Từ (5) và (6) suy ra AKOS là hình thoi.

Ta có ∆OAB vuông tại A có OA = 2OD = 2R

\[ \Rightarrow \widehat {OAB} = 30^\circ \Rightarrow \tan \widehat {OAB} = \tan 30^\circ = \frac{{KI}}{{AI}}\]

\[ \Rightarrow KI = \tan 30^\circ .AI = \frac{{\sqrt 3 }}{3}R\]

\[ \Rightarrow KS = \frac{{2\sqrt 3 }}{3}R\].

Vậy \[SAKOS = \frac{{OA.SK}}{2} = \frac{{2R.\frac{{2\sqrt 3 }}{3}R}}{2} = \frac{{2\sqrt 3 }}{3}{R^2}.\]