Câu hỏi trong đề: Giải SGK Toán 8 Cánh diều Bài 16. Hình thang cân có đáp án !!
Quảng cáo
Trả lời:
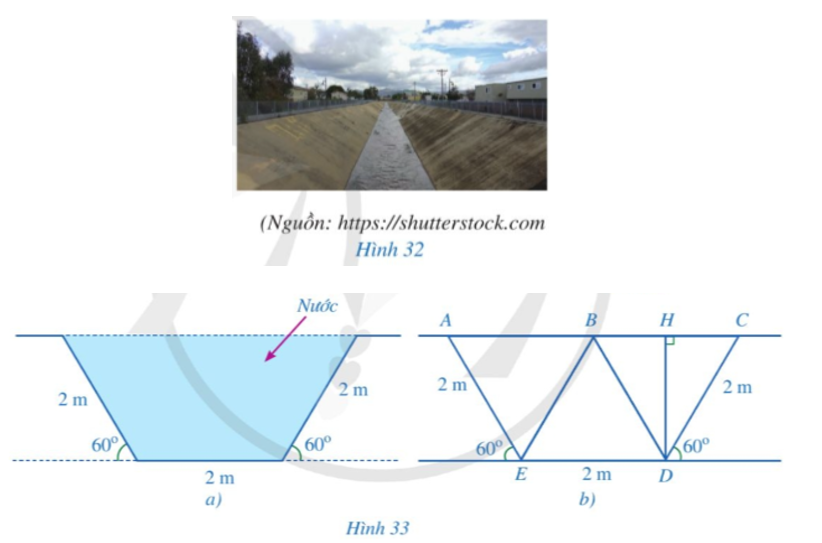
b) • Do ΔBCD là tam giác đều nên đường cao BH đồng thời là đường trung tuyến của tam giác
Do đó H là trung điểm của BC nên .
Xét ΔDHC vuông tại H, theo định lí Pythagore có:
CD2 = HC2 + DH2
Suy ra DH2 = CD2 – HC2 = 22 – 12 = 3.
Do đó DH = (m).
• Do ΔABE là tam giác đều nên AB = AE = 2 m.
Khi đó AC = AB + BC = 2 + 2 = 4 (m).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
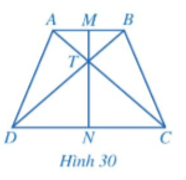
a) Do ABCD là hình thang cân nên AC = BD và AD = BC (tính chất hình thang cân).
Xét ΔADC và ΔBCD có:
AD = BC; AC = BD; DC là cạnh chung
Do đó ΔADC = ΔBCD (c.c.c)
Suy ra (hai góc tương ứng)
Hay .
Chứng minh tương tự ta cũng có: ΔABD = ΔBAC (c.c.c)
Suy ra (hai góc tương ứng)
Hay .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.