Cho (O; R), lấy điểm A cách O một khoảng bằng 2R. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.
a) Chứng minh: ∆OBA vuông tại B và ∆OAK cân tại K.
b) Đường thẳng KI cắt AB tại M. Chứng minh rằng KM là tiếp tuyến của đường tròn (O).
c) Tính chu vi tam giác AMK theo R.

Lời giải

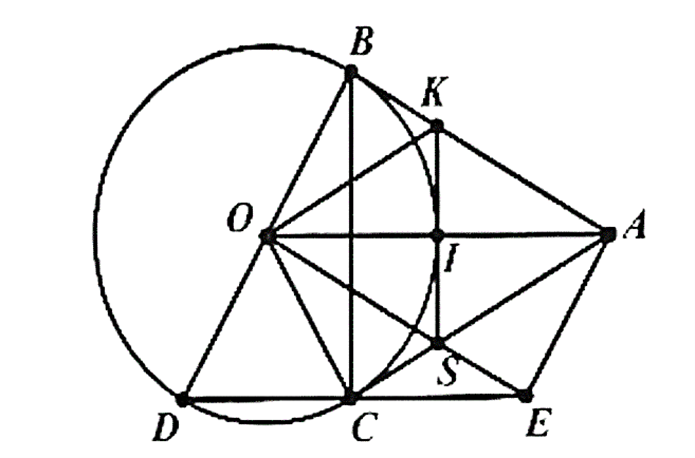
a) Ta có AB và AC là tiếp tuyến của (O) \( \Rightarrow \widehat {ABO} = \widehat {ACO} = 90^\circ \).

Xét tứ giác ABOC có:

\(\widehat {ABO} + \widehat {ACO} = 90^\circ + 90^\circ = 180^\circ \).

Suy ra tứ giác ABOC là tứ giác nội tiếp đường tròn.

Hay A, B, O, C thuộc 1 đường tròn.

b) Ta có: AB và AC là tiếp tuyến của (O) Þ AB = AC.

Mà OB = OC = R Þ OA là đường trung trực của BC hay OA ^ BC (1)

Xét ∆CBD nội tiếp (O) có BD là đường kính của (O).

Suy ra ∆CBD vuông tại C hay DC ^ BC (2)

Từ (1), (2) Þ DC // OA.

c) Ta có: DC // OA Þ CE // OA Þ OCEA là hình thang (3)

Ta có: \[\widehat {ODE} + \widehat {OBC} = 90^\circ \];

\(\widehat {OBC} + \widehat {BOA} = 90^\circ \).

Suy ra \(\widehat {ODE} = \widehat {BOA}\).

Xét ∆BOA và ∆ODE có:

\(\widehat {ODE} = \widehat {BOA}\) (cmt)

\[\widehat {DOE} = \widehat {OBA} = 90^\circ \]

OB = OD = R

Þ ∆BOA = ∆ODE (g.c.g)

Þ AB = OE (hai cạnh tương ứng)

Mà AB = AC (AB và AC đều là tiếp tuyến chung của (O))

Suy ra OE = AC (4)

Từ (3) và (4) Þ OCEA là hình thang cân.

d) Ta có: \[\widehat {SOI} + \widehat {AOB} = 90^\circ \]

\(\widehat {AOB} + \widehat {OAB} = 90^\circ \)

\(\widehat {OAB} = \widehat {SAO}\)

Suy ra \(\widehat {SOA} = \widehat {SAO}\) Þ ∆SOA cân tại S

Lại có SI là đường trung tuyến \(\left( {OI = IA = \frac{{OA}}{2} = R} \right)\)

Suy ra SI ^ OA Þ KS ^ OA (5)

Ta có ∆KAS có \(\widehat {KAI} = \widehat {SAI}\)

AI ^ KS suy ra KI = SI.

Mà OI ^ AI

Suy ra OKAS là hình bình hành (6)

Từ (5) và (6) suy ra AKOS là hình thoi.

Ta có ∆OAB vuông tại A có OA = 2OD = 2R

\[ \Rightarrow \widehat {OAB} = 30^\circ \Rightarrow \tan \widehat {OAB} = \tan 30^\circ = \frac{{KI}}{{AI}}\]

\[ \Rightarrow KI = \tan 30^\circ .AI = \frac{{\sqrt 3 }}{3}R\]

\[ \Rightarrow KS = \frac{{2\sqrt 3 }}{3}R\].

Vậy \[SAKOS = \frac{{OA.SK}}{2} = \frac{{2R.\frac{{2\sqrt 3 }}{3}R}}{2} = \frac{{2\sqrt 3 }}{3}{R^2}.\]