Câu hỏi:
12/07/2024 493
Giải phương trình \(\sin 2x + \cos \left( {6x + \frac{\pi }{3}} \right) = 0\).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
\(\sin 2x + \cos \left( {6x + \frac{\pi }{3}} \right) = 0\)
\( \Leftrightarrow \cos \left( {6x + \frac{\pi }{3}} \right) = - \sin 2x\)
\[ \Leftrightarrow \cos \left( {6x + \frac{\pi }{3}} \right) = \cos \left( {2x + \frac{\pi }{2}} \right)\]
\( \Leftrightarrow \left[ \begin{array}{l}6x + \frac{\pi }{3} = 2x + \frac{\pi }{2} + k2\pi \\6x + \frac{\pi }{3} = - 2x - \frac{\pi }{2} + k2\pi \end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}4x = \frac{\pi }{6} + k2\pi \\8x = - \frac{{5\pi }}{6} + k2\pi \end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{24}} + k\frac{\pi }{2}\\x = - \frac{{5\pi }}{{48}} + k\frac{\pi }{4}\end{array} \right.\).
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một hộp đựng 8 viên bi màu xanh, 5 viên bi đỏ, 3 viên bi màu vàng. Có bao nhiêu cách chọn từ hộp đó ra 4 viên bi trong đó có đúng 2 viên bi xanh?
Xem đáp án »
12/07/2024
20,322
Câu 3:
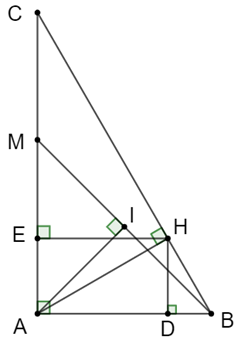
Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AB = 4 cm, \(AC = 4\sqrt 3 \;cm\). Giải tam giác ABC.
b) Kẻ HD, HE lần lượt vuông góc với AB, AC (D thuộc AB, E thuộc AC). Chứng
minh BD.DA + CE.EA = AH2.
c) Lấy diểm M nằm giữa E và C, kẻ AI vuông góc với MB tại I. Chứng minh:
\[\sin \widehat {AMB}\,.\,\sin \widehat {ACB} = \frac{{HI}}{{CM}}\].
Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AB = 4 cm, \(AC = 4\sqrt 3 \;cm\). Giải tam giác ABC.
b) Kẻ HD, HE lần lượt vuông góc với AB, AC (D thuộc AB, E thuộc AC). Chứng
minh BD.DA + CE.EA = AH2.
c) Lấy diểm M nằm giữa E và C, kẻ AI vuông góc với MB tại I. Chứng minh:
\[\sin \widehat {AMB}\,.\,\sin \widehat {ACB} = \frac{{HI}}{{CM}}\].
Xem đáp án »
12/07/2024
14,550
Câu 4:
Cho bốn điểm A, B, C, D. Chứng minh:
a) \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \);
b) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 \).
Cho bốn điểm A, B, C, D. Chứng minh:
a) \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \);
b) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 \).
Xem đáp án »
12/07/2024
10,847
Câu 5:
Cho đường tròn tâm O đường kính BC, điểm A thuộc đường tròn. Vẽ bán kính OK song song với BA (K và A nằm cùng phía đối với BC) tiếp tuyến đường trong tâm O tại C cắt ở I , OI cắt tại H.
a) Chứng minh tam giác ABC là tam giác vuông tại A.
b) Chứng minh IA là tiếp tuyến của đường tròn tâm O.
c) Cho BC = 30 cm; AB = 18 cm, tính các độ dài OI và CI.
Cho đường tròn tâm O đường kính BC, điểm A thuộc đường tròn. Vẽ bán kính OK song song với BA (K và A nằm cùng phía đối với BC) tiếp tuyến đường trong tâm O tại C cắt ở I , OI cắt tại H.
a) Chứng minh tam giác ABC là tam giác vuông tại A.
b) Chứng minh IA là tiếp tuyến của đường tròn tâm O.
c) Cho BC = 30 cm; AB = 18 cm, tính các độ dài OI và CI.
Xem đáp án »
12/07/2024
10,825
Câu 6:
Một cái thang dài 4 m đang dựa vào tường, chân thang cách chân tường 2 m. Tính góc tạo bởi thang với mặt đất và với mặt tường.
Xem đáp án »
12/07/2024
9,614
Câu 7:
Cho tam giác ABC. Chứng minh nếu b + c = 2a thì \[\frac{2}{{{h_a}}} = \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}}\].
Xem đáp án »
12/07/2024
7,395
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận