Một lớp học cuối năm xếp học lực có ba loại: Giỏi, khá, trung bình. Số học sinh khá bằng 50% số học sinh cả lớp, số học sinh trung bình bằng \(\frac{2}{5}\) số học sinh cả lớp, số học sinh giỏi là 5 em.

a) Hỏi lớp có bao nhiêu học sinh?

b) Tính tỉ số phần trăm của số học sinh mỗi loại so với số học sinh cả lớp?

Lời giải

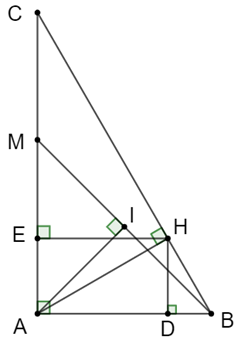
a) ∆ABC vuông tại A

\( \Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{4^2} + {{\left( {4\sqrt 3 } \right)}^2}} = 8\;(cm)\)

\(\sin \widehat {ACB} = \frac{{AB}}{{BC}} = \frac{4}{8} = \frac{1}{2} \Rightarrow \widehat {ACB} = 30^\circ \)

\( \Rightarrow \widehat {ABC} = 180^\circ - \widehat {BAC} - \widehat {ACB} = 180^\circ - 90^\circ - 30^\circ = 60^\circ \)

b) Tứ giác ADHE có \(\widehat A = \widehat D = \widehat E = 90^\circ \) nên tứ giác ADHE là hình chữ nhật

Þ DE = AH và \(\widehat {DHE} = 90^\circ \)

Þ ∆DHE vuông tại H Þ DH² + EH² = DE²

Xét ∆ADH và ∆HDB có:

\(\widehat {ADH} = \widehat {HDB}\;\left( { = {{90}^ \circ }} \right)\)

\(\widehat {DAH} = \widehat {DHB}\) (cùng phụ \(\widehat {AHD}\))

Do đó ∆ADH ᔕ ∆HDB (g.g)

\( \Rightarrow \frac{{EA}}{{EH}} = \frac{{EH}}{{CE}} \Rightarrow EA.EC = E{H^2}\)

Þ BD.DA + CE.EA = DH² + EH² = DE² = AH².

Vậy BD.DA + CE.EA = AH² (đpcm).

c) Ta có \(\widehat {AIB} = \widehat {AHB} = 90^\circ \) nên I, H thuộc đường tròn đường kính AB

Þ Tứ giác ABHI nội tiếp đường tròn đường kính AB

\( \Rightarrow \widehat {BAH} = \widehat {BIH}\) (góc nội tiếp chắn cung BM)

Mà \(\widehat {BAH} = \widehat {BCM}\) (cùng phụ \(\widehat {CAM}\))

Nên \(\widehat {BIH} = \widehat {BCM}\)

• Xét ∆BIH và ∆BCM có:

\(\widehat B\) chung

\(\widehat {BIH} = \widehat {BCM}\) (cmt)

Do đó ∆BIH ᔕ ∆BCM (g.g)

Suy ra \(\frac{{BH}}{{BM}} = \frac{{HI}}{{CM}}\) (các cạnh tương ứng tỉ lệ)

• Xét ∆BAM và ∆BCA có:

\(\widehat B\) chung

\(\widehat {BMA} = \widehat {BAC}\;\left( { = {{90}^ \circ }} \right)\) (cmt)

Do đó ∆BAM ᔕ ∆BCA (g.g)

\( \Rightarrow \frac{{BH}}{{BA}} = \frac{{AB}}{{BC}} \Rightarrow BH = \frac{{A{B^2}}}{{BC}} \Rightarrow \frac{{A{B^2}}}{{BC.BM}} = \frac{{HI}}{{CM}}\)

Khi đó \(\sin \widehat {AMB}\,\,.\,\,\sin \widehat {ACB} = \frac{{AB}}{{BM}}\,.\,\frac{{AB}}{{BC}} = \frac{{A{B^2}}}{{BM\,.\,BC}} = \frac{{HI}}{{CM}}\).

Vậy \[\sin \widehat {AMB}\,.\,\sin \widehat {ACB} = \frac{{HI}}{{CM}}\] (đpcm).