Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
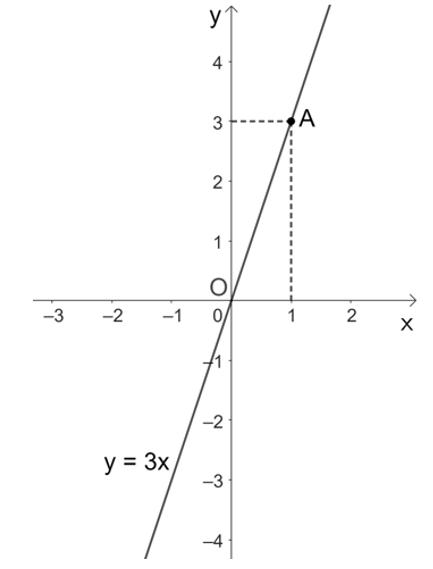
a) Đồ thị hàm số y = 3x.
Với x = 1 thì y = 3 . 1 = 3, ta được điểm A(1; 3) thuộc đồ thị của hàm số y = 3x.
Vậy đồ thị của hàm số y = 3x là đường thẳng đi qua hai điểm O(0; 0) và A(1; 3).
Khi đó, đồ thị hàm số y = 3x được biểu diễn như hình vẽ:
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng – 1 và đi qua điểm M(1; 2). Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng – 1 và đi qua điểm M(1; 2). Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
Xem đáp án »
12/07/2024
10,032
Câu 2:
b) Xác định đường thẳng y = ax + b (a ≠ 0) đi qua điểm M(1; 3) và song song với đường thẳng y = 2x – 1. Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
b) Xác định đường thẳng y = ax + b (a ≠ 0) đi qua điểm M(1; 3) và song song với đường thẳng y = 2x – 1. Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
Xem đáp án »
12/07/2024
9,263
Câu 3:
Vẽ đồ thị của các hàm số y = 3x; y = 3x + 4; trên cùng một mặt phẳng tọa độ.
Vẽ đồ thị của các hàm số y = 3x; y = 3x + 4; trên cùng một mặt phẳng tọa độ.
Xem đáp án »
12/07/2024
5,414
Câu 5:
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về đường thẳng d là đồ thị của hàm số y = ax + b (a ≠ 0)?
a) Đường thẳng d cắt trục tung tại điểm có tung độ bằng .
b) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng b.
c) Đường thẳng d cắt trục tung tại điểm có tung độ bằng b.
d) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng .
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về đường thẳng d là đồ thị của hàm số y = ax + b (a ≠ 0)?
a) Đường thẳng d cắt trục tung tại điểm có tung độ bằng .
b) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng b.
c) Đường thẳng d cắt trục tung tại điểm có tung độ bằng b.
d) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng .
Xem đáp án »
11/07/2024
3,666
Câu 6:
Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong số các đường thẳng sau: y = – 2x + 5; y = – 2x; y = 4x – 1.
Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong số các đường thẳng sau: y = – 2x + 5; y = – 2x; y = 4x – 1.
Xem đáp án »
12/07/2024
2,896
về câu hỏi!