Cho ∆ABC cân tại A. Qua B kẻ đường thẳng vuông góc với AB, qua C kẻ đường thẳng vuông góc với AC, chúng cắt nhau ở D. Chứng minh:

a. ∆BDC cân.

b. AD là tia phân giác của góc A và DA là tia phân giác của \(\widehat D\).

c. AD ⊥ BC và AD đi qua trung điểm của BC.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a. Do ∆ABC cân \(\widehat {ABC} = \widehat {ACB}\)

\(\widehat {DBC} + \widehat {ABC} = \widehat {DCB} + \widehat {ACB} = 90^\circ \Rightarrow \widehat {DBC} = \widehat {DCB} \Rightarrow \Delta BDC\) cân tại D

b. Ta có ∆BDC cân nên BD = CD

∆ABC cân nên AB = AC

⇒ ∆ABD = ∆ACD (Hai tam giác vuông có các cạnh góc vuông tương ứng bằng nhau)

\( \Rightarrow \widehat {BAD} = \widehat {CAD};\widehat {BDA} = \widehat {CDA} \Rightarrow AD\) là phân giác của \(\widehat A\) và \(\widehat D\)

c. Do ∆ABC cân tại A và AD lầ phân giác \(\widehat A\) nên AD là đường cao đồng thời là đường trung tuyến thuộc cạnh BC của ∆ABC (Trong tam giác cân đường phân giác đồng thời là đường cao, đường trung tuyến và đường trung trực)

⇒ AD ⊥ BC và đi qua trung điểm của BC.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của các đoạn BC, CD, SO. Tìm giao tuyến của (MNP) với các mặt phẳng (SAB), (SAD), (SBC) và (SCD).

Xem đáp án

Lời giải

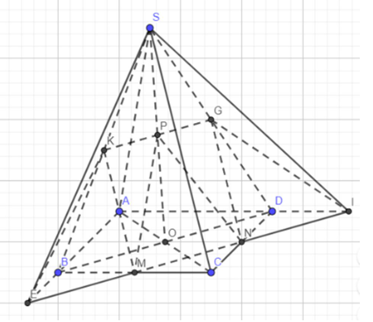
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần (ảnh 1)

Gọi I, E lần lượt là giao điểm của MN với AD, AB

Qua P kẻ đường thẳng song song với BD cắt SB, SD lần lượt tại K, G

Ta có:

M, N lần lượt là trung điểm của BC, CD ⇒ MN là đường trung bình của ∆BCD ⇒ MN // BD

Mà KG // BD ⇒ MN // KG ⇒ K, G ∈ (MNP)

Ta có:

+) \(\left\{ {\begin{array}{*{20}{c}}{E = AB \cap MN \Rightarrow E \in \left( {SAB} \right) \cap \left( {MNP} \right)}\\{K \in SB;K \in \left( {MNP} \right) \Rightarrow K \in \left( {SAB} \right) \cap \left( {MNP} \right)}\end{array}} \right. \Rightarrow \left( {SAB} \right) \cap \left( {MNP} \right) = KE\)

+) \(\left\{ {\begin{array}{*{20}{c}}{I = AD \cap MN \Rightarrow I \in \left( {SAD} \right) \cap \left( {MNP} \right)}\\{G \in SD;G \in \left( {MNP} \right) \Rightarrow G \in \left( {SAD} \right) \cap \left( {MNP} \right)}\end{array}} \right. \Rightarrow \left( {SAD} \right) \cap \left( {MNP} \right) = IG\)

+) \(\left\{ {\begin{array}{*{20}{c}}{M,K \in \left( {MNP} \right)}\\{M,K \in \left( {SBC} \right)}\end{array}} \right. \Rightarrow \left( {SBC} \right) \cap \left( {MNP} \right) = MK\)

+) \(\left\{ {\begin{array}{*{20}{c}}{N,G \in \left( {MNP} \right)}\\{N,G \in \left( {SCD} \right)}\end{array}} \right. \Rightarrow \left( {SCD} \right) \cap \left( {MNP} \right) = NG\)

Vậy (SAB) ∩ (MNP) = KE; (SAD) ∩ (MNP) = IG; (SBC) ∩ (MNP) = MK; (SCD) ∩ (MNP) = NG.

Câu 2

Tính tổng: \({\sin ^2}2^\circ + {\sin ^2}4^\circ + {\sin ^2}6^\circ + ... + {\sin ^2}84^\circ + {\sin ^2}86^\circ + {\sin ^2}88^\circ \).

Xem đáp án

Lời giải

\({\sin ^2}2^\circ + {\sin ^2}4^\circ + {\sin ^2}6^\circ + ... + {\sin ^2}84^\circ + {\sin ^2}86^\circ + {\sin ^2}88^\circ \)

\( = \left( {{{\sin }^2}2^\circ + {{\sin }^2}88^\circ } \right) + \left( {{{\sin }^2}4^\circ + {{\sin }^2}86^\circ } \right) + ... + \left( {{{\sin }^2}44^\circ + {{\sin }^2}46^\circ } \right)\)

\( = \left( {{{\sin }^2}2^\circ + {{\cos }^2}2^\circ } \right) + \left( {{{\sin }^2}4^\circ + {{\cos }^2}4^\circ } \right) + ... + \left( {{{\sin }^2}44^\circ + {{\cos }^2}44^\circ } \right)\) (do 2 góc phụ nhau sin góc này bằng cos góc kia)

= 1 + 1 + 1 +....+ 1 = 22 .

Câu 3