Trong mặt phẳng tọa độ (Oxy), cho phép biến hình F có biểu thức tọa độ \(x' = \frac{{ - 3x + 4y}}{5};y' = \frac{{4x + 3y}}{5}\). Ảnh của \(\Delta :x + y = 0\) qua phép biến hình F là ?
Trong mặt phẳng tọa độ (Oxy), cho phép biến hình F có biểu thức tọa độ \(x' = \frac{{ - 3x + 4y}}{5};y' = \frac{{4x + 3y}}{5}\). Ảnh của \(\Delta :x + y = 0\) qua phép biến hình F là ?
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{5x' = - 3x + 4y}\\{5y' = 4x + 3y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{15x' = - 9x + 12y}\\{20y' = 16x + 12y}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{25x = 20y' - 15x'}\\{4y = 5x' + 3x}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5x = 4y' - 3x'}\\{20y = 25x' + 15x}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5x = 4y' - 3x'}\\{20y = 25x' + 3\left( {4y' - 3x'} \right)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5x = 4y' - 3x'}\\{20y = 16x' + 12y'}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5x = 4y' - 3x'}\\{5y = 4x' + 3y'}\end{array}} \right.\)
∆: x + y = 0 ⟺ 5x + 5y = 0
\( \Leftrightarrow 4y' - 3x' + 4x' + 3y' = 0 \Leftrightarrow x' + 7y' = 0\)
\( \Rightarrow \Delta ':x + 7y = 0\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
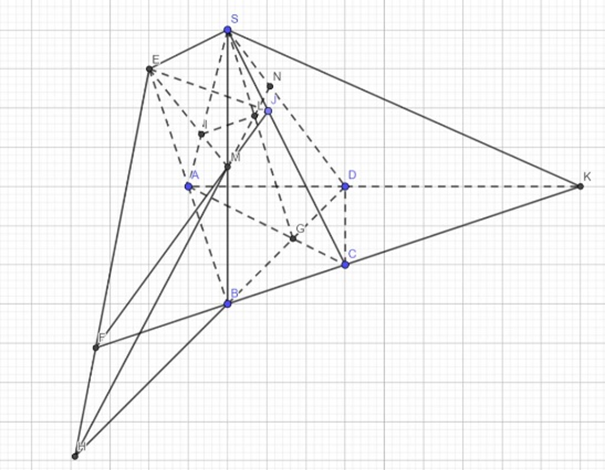
a. Gọi \(AD \cap BC = K \Rightarrow \left( {SAD} \right) \cap \left( {SBC} \right) = SK\)
b. Gọi \(IM \cap AB = E \Rightarrow AB \cap \left( {IJM} \right) = E\)
c. Gọi \(JM \cap BC = F \Rightarrow BC \cap \left( {IJM} \right) = F\)
d. Gọi \(AC \cap BD = G,AG \cap IJ = L,ML \cap SD = N \Rightarrow N = SD \cap \left( {IJM} \right)\)
e. Ta có: \(MN \cap BD = H \Rightarrow H \in \left( {MIJ} \right),H \in \left( {ABCD} \right) \Rightarrow H \in \left( {MNJ} \right) \cap \left( {ABCD} \right)\)(Hay H thuộc giao tuyến của \(\left( {MNJ} \right);\left( {ABCD} \right)\)
Lại có \(E \in \left( {MIJ} \right) \Rightarrow E \in \left( {MNJ} \right),E \in AB \Rightarrow E \in \left( {ABCD} \right)\)
\(F \in MJ \Rightarrow F \in \left( {MNJ} \right) \cap \left( {ABCD} \right)\)⇒ H, E, F thẳng hàng (cùng thuộc giao tuyến của (MNJ) và (ABCD).
Lời giải
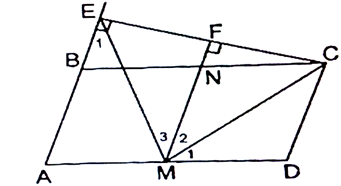
a. Ta có: MN // AB // CD (MN và AB cùng vuông góc với CE) và MD // NC (AD // BC)
⇒ MNCD là hình bình hành (1)
MD = \(\frac{{AD}}{2}\); MN = AB = \(\frac{{AD}}{2}\) nên MD = MN (2)
Từ (1) và (2) ⇒ MNCD là hình thoi.
b. Do MN // AB // CD (câu a) và M là trung điểm AD
⇒ F là trung điểm EC ⇒ MF là đường trung tuyến của ∆MEC với lại MF là đường cao của ∆MEC (MF ⊥ EC) ⇒ ∆MEC cân tại M
c. ∆MEC cân tại M và MF là đường cao của ∆MEC
⇒ MF là đường phân giác của ∆MEC \( \Rightarrow \widehat {EMF} = \widehat {FMC}\)
\(\widehat {AEM} = \widehat {EMF}\) (AB // MN); \(\widehat {FMC} = \widehat {CMD}\)(MNCD là hình thoi nên đường chéo MC là phân giác
Từ 3 điều trên \( \Rightarrow \widehat {AEM} = \widehat {EMF} = \widehat {FMC} = \widehat {CMD} \Rightarrow 2\widehat {AEM} = \widehat {FMC} + \widehat {CMD}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.