Câu hỏi:
12/07/2024 1,921
Cho (O) đường kính AB = 10cm, C là 1 điểm trên đường tròn (O) sao cho AC = 6cm. Vẽ CH vuông góc với AB (H thuộc AB).
a) Tính AH và góc ABC.
b) Tiếp tuyến tại B và C của (O) cắt nhau tại D. Chứng minh rằng OD vuông góc với BC.
c) Tiếp tuyến tại A của (O) cắt BC tại E. Chứng minh CE.CB = AH.AB.
d) Gọi I là trung điểm của CH tia BI cắt AE tại F. Chứng minh FC là tiếp tuyến của (O).
Cho (O) đường kính AB = 10cm, C là 1 điểm trên đường tròn (O) sao cho AC = 6cm. Vẽ CH vuông góc với AB (H thuộc AB).
a) Tính AH và góc ABC.
b) Tiếp tuyến tại B và C của (O) cắt nhau tại D. Chứng minh rằng OD vuông góc với BC.
c) Tiếp tuyến tại A của (O) cắt BC tại E. Chứng minh CE.CB = AH.AB.
d) Gọi I là trung điểm của CH tia BI cắt AE tại F. Chứng minh FC là tiếp tuyến của (O).
Câu hỏi trong đề:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
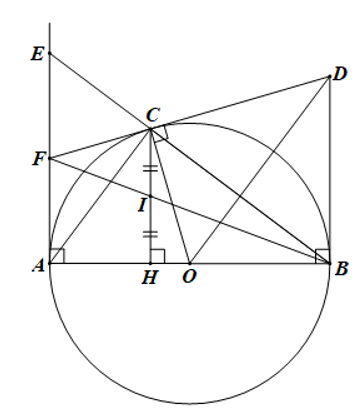
a) Xét DABC có C thuộc đường tròn đường kính AB nên
Do đó DABC vuông tại C.
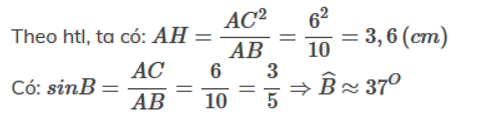
b) Do DB, DC là tiếp tuyến với đường tròn suy ra DB = DC nên D thuộc đường trung trực của BC.
Ta có OB = OC nên O thuộc đường trung trực của BC.
Do đó OD là đường trung trực của BC.
Þ OD ⊥ BC.
c) Áp dụng hệ thức lượng cho tam giác vuông EAB ta có: AC2 = CE.CB
Áp dụng hệ thức lượng cho tam giác vuông ABC ta có: AC2 = AH.AB
Suy ra CE.CB = AH.AB.
d) Ta có: CH ⊥ AB, EA ⊥ AB nên CH // AB.
Xét DABF có IH // FA, theo hệ quả định lí Thalès ta có:.
Xét DEBF có CI // EF, theo hệ quả định lí Thalès ta có: .
, mà IH = CI (do I là trung điểm của CH)
Þ FA = EF, hay F là trung điểm của AE
Xét DACE vuông tại C có đường trung tuyến CF nên FA = FC = FE.
Xét DOAF và DOCF có:
FA = FC (cmt); FO là cạnh chung; OA = OC (cùng bằng bán kính)
Do đó DOAF = DOCF (c.c.c)
Þ FC ⊥ OC, mà C thuộc đường tròn (O)
Do đó FC là tiếp tuyến của (O).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Một người đứng trên tháp quan sát của ngọn hải đăng cao 50 m nhìn về hướng Tây Nam, người đó quan sát hai lần một con thuyền đang hướng về ngọn hải đăng. Lần thứ nhất người đó nhìn thấy thuyền với góc hạ là 20°, lần thứ 2 người đó nhìn thấy thuyền với góc hạ là 30°. Hỏi con thuyền đã đi được bao nhiêu mét giữa hai lần quan sát? (làm tròn đến chữ số thập phân thứ nhất)
Một người đứng trên tháp quan sát của ngọn hải đăng cao 50 m nhìn về hướng Tây Nam, người đó quan sát hai lần một con thuyền đang hướng về ngọn hải đăng. Lần thứ nhất người đó nhìn thấy thuyền với góc hạ là 20°, lần thứ 2 người đó nhìn thấy thuyền với góc hạ là 30°. Hỏi con thuyền đã đi được bao nhiêu mét giữa hai lần quan sát? (làm tròn đến chữ số thập phân thứ nhất)
Xem đáp án »
12/07/2024
12,280
Câu 3:
Một mảnh đất hình chữ nhật bị xén đi một góc (hình vẽ), phần còn lại có dạng hình tứ giác ABCD với độ dài các cạnh là AB = 15m, BC = 19m, CD = 10m, DA = 20m. Diện tích mảnh đất ABCD bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị).
Một mảnh đất hình chữ nhật bị xén đi một góc (hình vẽ), phần còn lại có dạng hình tứ giác ABCD với độ dài các cạnh là AB = 15m, BC = 19m, CD = 10m, DA = 20m. Diện tích mảnh đất ABCD bằng bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị).
Xem đáp án »
12/07/2024
10,926
Câu 4:
Cho (O), điểm A ở bên ngoài đường tròn. Vẽ các tiếp tuyến AB, AC và cát tuyến ADE. Gọi H là trung điểm của DE.
a) Chứng minh 5 điểm A, B, H, O, C cùng thuộc 1 đường tròn.
b) Chứng minh HA là tia phân giác của góc BHC.
c) Gọi I là giao của BC và DE. Chứng minh AB2 = AI.AH.
d) BH cắt (O) ở K. Chứng minh AE // CK.
Cho (O), điểm A ở bên ngoài đường tròn. Vẽ các tiếp tuyến AB, AC và cát tuyến ADE. Gọi H là trung điểm của DE.
a) Chứng minh 5 điểm A, B, H, O, C cùng thuộc 1 đường tròn.
b) Chứng minh HA là tia phân giác của góc BHC.
c) Gọi I là giao của BC và DE. Chứng minh AB2 = AI.AH.
d) BH cắt (O) ở K. Chứng minh AE // CK.
Xem đáp án »
12/07/2024
6,827
Câu 5:
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh hai tam giác ABM và ACM bằng nhau.
b) Chứng minh AM vuông góc với BC.
c) Chứng minh AM là phân giác của góc A.
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.
a) Chứng minh hai tam giác ABM và ACM bằng nhau.
b) Chứng minh AM vuông góc với BC.
c) Chứng minh AM là phân giác của góc A.
Xem đáp án »
12/07/2024
5,275
Câu 6:
Cho đường tròn (O) dây cung BC (BC không là đường kính). Điểm A di động trên cung nhỏ BC (A khác B và C, độ dài cạnh AB khác AC). Kẻ đường kính AA' của đường tròn (O), D là chân đường vuông góc kẻ từ A đến BC. Hai điểm E, F lần lượt là chân đường vuông góc kẻ từ B, C đến AA'.
a) Chứng minh rằng 4 điểm A, B, D, E cùng nằm trên 1 đường tròn.
b) Chứng minh BD.AC = AD.A'C.
Cho đường tròn (O) dây cung BC (BC không là đường kính). Điểm A di động trên cung nhỏ BC (A khác B và C, độ dài cạnh AB khác AC). Kẻ đường kính AA' của đường tròn (O), D là chân đường vuông góc kẻ từ A đến BC. Hai điểm E, F lần lượt là chân đường vuông góc kẻ từ B, C đến AA'.
a) Chứng minh rằng 4 điểm A, B, D, E cùng nằm trên 1 đường tròn.
b) Chứng minh BD.AC = AD.A'C.
Xem đáp án »
12/07/2024
5,218
Câu 7:
Một lớp học có 40 học sinh trong đó có 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh. Xác suất của biến cố C: “Học sinh được chọn không giỏi Văn và Toán” là:
Một lớp học có 40 học sinh trong đó có 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh. Xác suất của biến cố C: “Học sinh được chọn không giỏi Văn và Toán” là:
Xem đáp án »
09/05/2023
4,226
về câu hỏi!