Câu hỏi:

12/07/2024 5,868

Cho ∆ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:

a. AC = EB và AC // BE.

b. Gọi I là một điểm trên AC, K là một điểm trên EB sao cho: AI = EK. Chứng minh: I, M, K thẳng hàng.

c. Từ E kẻ EH ⊥ BC (H ∈ BC). Biết \(\widehat {HBE}\)= 50\(^\circ \), \(\widehat {MEB}\) = 25\(^\circ \), tính \(\widehat {HEM}\) và \(\widehat {BME}\).

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

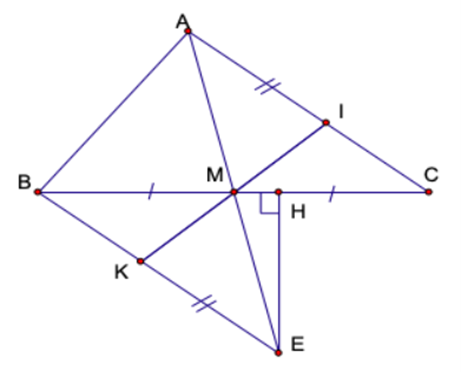
Media VietJack

a. Xét ∆AMC và ∆EMB có: AM = EM (gt); \(\widehat {AMC} = \widehat {EMB}\)(đối đỉnh); BM = MC (gt)

Nên: ∆AMC = ∆EMB (c.g.c) ⇒ AC = EB

Vì ∆AMC = ∆EMB ⇒ \(\widehat {MAC} = \widehat {MEB}\)(2 góc có vị trí so le trong được tạo bởi đường thẳng AC và EB cắt đường thẳng AE) ⇒ AC // BE

b. Xét ∆AMI và ∆EMK có: AM = EM (gt); \(\widehat {MAI} = \widehat {MEK}\)(vì ∆AMC = ∆EMB); AI = EK (gt) nên ∆AMI = ∆EMK (c.g.c) ⇒ \(\widehat {AMI} = \widehat {EMK}\)

Mà \(\widehat {AMI} + \widehat {IME} = 180^\circ \) (tính chất 2 góc kề bù)

⇒ \(\widehat {EMK} + \widehat {IME} = 180^\circ \) ⇒ 3 điểm I, M, K thẳng hàng

c. Trong tam giác vuông BHE \(\left( {\widehat H = 90^\circ } \right)\) có \(\widehat {HBE} = 50^\circ \)

\( \Rightarrow \widehat {HBE} = 90^\circ - \widehat {HBE} = 90^\circ - 50^\circ = 40^\circ \)

\( \Rightarrow \widehat {HEM} = \widehat {HEB} - \widehat {MEB} = 40^\circ - 25^\circ = 15^\circ \)

\(\widehat {BME}\) là góc ngoài tại đỉnh M của ∆HEM

Nên \(\widehat {BME} = \widehat {HEM} + \widehat {MHE} = 15^\circ + 90^\circ = 105^\circ \) (định lý góc ngoài của tam giác).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

Xem thêm ...

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi O là giao điểm của AD và BC; gọi E là giao điểm của AC và BD. Chứng minh:

a) ∆AOB cân tại O.

b) ∆ABD = ∆BAC.

c) EC = ED.

d) OE là đường trung trực chung của AB và CD.

Xem đáp án

Lời giải

Lời giải:

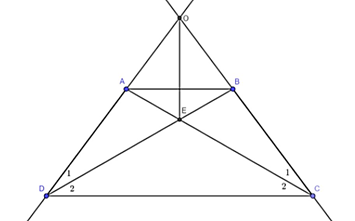
Media VietJack

a) ABCD là hình thang cân

\( \Rightarrow \widehat {BCD} = \widehat {ADC} \Leftrightarrow \widehat {OCD} = \widehat {ODC}\)

\(\Delta ODC,\widehat {OCD} = \widehat {ODC}\)

⇒ ΔODC cân tại O ⇒ OC = OD

Mà AD = BC (ABCD là hình thang cân) ⇒ OA = OB ⇒ ΔOAB cân tại O

b) ABCD là hình thang cân

\( \Rightarrow \widehat {BAD} = \widehat {ABC}\)

Xét ∆BAD và ∆ABC: BA chung; AD = BC; \(\widehat {BAD} = \widehat {ABC} \Rightarrow \Delta BAD = \Delta ABC\)

c) ∆BAD = ∆ABC \( \Rightarrow \widehat {{D_1}} = \widehat {{C_1}}\)

Mà \(\widehat {ADC} = \widehat {BCD} \Rightarrow \widehat {{D_2}} = \widehat {{C_2}}\)

⇒ ΔDEC cân tại E

d) EC = ED

Mà AC = BD (ABCD là hình thang cân)

⇒ EA = EB

Lại có OA = OB

⇒ OE là đường trung trực AB

OD = OC; EC = ED

⇒ OE là đường trung trực CD.

Câu 2

Cho ∆ABC có a = 7, b = 8, c = 5. Tính số đo góc A, diện tích S của tam giác ABC, đường cao kẻ từ đỉnh A là h_a và bán kính R của đường tròn ngoại tiếp tam giác ABC.

Xem đáp án

Lời giải

Lời giải:

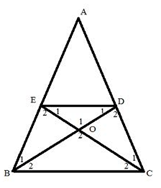
Media VietJack

Theo hệ quả của định lí côsin ta có:

\[\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{8^2} + {5^2} - {7^2}}}{{2.8.5}} = \frac{1}{2}\]

\( \Rightarrow \widehat A = 60^\circ \).

Diện tích tam giác ABC là \(S = \frac{1}{2}bc\sin A = \frac{1}{2}.8.5.\sin 60^\circ = 10\sqrt 3 \).

Vì \(S = \frac{1}{2}a{h_a}\) nên \({h_a} = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{7} = \frac{{20\sqrt 3 }}{7}\)

Lại có: \(S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{7.8.5}}{{4.10\sqrt 3 }} = \frac{{7\sqrt 3 }}{3}\).

Câu 3