Cho hàm số y = 2x – 3 có đồ thị (d) và điểm A(–1; –5). a) Viết phương trình đường thẳng d1 qua A và song song với trục Ox . b) Viết phương trình đường thẳng d2 qua A và song song với đường thẳng d. c...

Câu hỏi:

11/07/2024 177

Cho hàm số y = 2x – 3 có đồ thị (d) và điểm A(–1; –5).

a) Viết phương trình đường thẳng d₁ qua A và song song với trục Ox .

b) Viết phương trình đường thẳng d₂ qua A và song song với đường thẳng d.

c) Viết phương trình đường thẳng d₃ qua A và vuông góc với đường thẳng d.

d) Viết phương trình đường thẳng d₄ qua A và gốc tọa độ.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

Gọi các đường thẳng có công thức chung là y = ax + b.

a. Đường thẳng d₁ qua A và song song với trục Ox

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - a + b = - 5}\\{a = 0;b \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 0}\\{b = - 5}\end{array}} \right. \Leftrightarrow \left( {{d_1}} \right):y = - 5\)

b. Đường thẳng d₂ qua A và song song với đường thẳng d

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - a + b = 5}\\{a = 2;b \ne - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = 7}\end{array}} \right. \Leftrightarrow y = 2x + 7\)

c. Đường thẳng d₃ qua A và vuông góc với đường thẳng d

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - a + b = 5}\\{2a = - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 2}\\{b = 3}\end{array}} \right. \Leftrightarrow \left( {{d_3}} \right):y = - 2x + 3\)

d. Đường thẳng d₄ qua A và gốc tọa độ

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - a + b = 5}\\{b = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 5}\\{b = 0}\end{array}} \right. \Leftrightarrow \left( {{d_4}} \right):y = - 5x\)

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi O là giao điểm của AD và BC; gọi E là giao điểm của AC và BD. Chứng minh:

a) ∆AOB cân tại O.

b) ∆ABD = ∆BAC.

c) EC = ED.

d) OE là đường trung trực chung của AB và CD.

Xem đáp án

Lời giải

Lời giải:

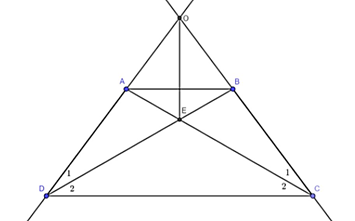
Media VietJack

a) ABCD là hình thang cân

\( \Rightarrow \widehat {BCD} = \widehat {ADC} \Leftrightarrow \widehat {OCD} = \widehat {ODC}\)

\(\Delta ODC,\widehat {OCD} = \widehat {ODC}\)

⇒ ΔODC cân tại O ⇒ OC = OD

Mà AD = BC (ABCD là hình thang cân) ⇒ OA = OB ⇒ ΔOAB cân tại O

b) ABCD là hình thang cân

\( \Rightarrow \widehat {BAD} = \widehat {ABC}\)

Xét ∆BAD và ∆ABC: BA chung; AD = BC; \(\widehat {BAD} = \widehat {ABC} \Rightarrow \Delta BAD = \Delta ABC\)

c) ∆BAD = ∆ABC \( \Rightarrow \widehat {{D_1}} = \widehat {{C_1}}\)

Mà \(\widehat {ADC} = \widehat {BCD} \Rightarrow \widehat {{D_2}} = \widehat {{C_2}}\)

⇒ ΔDEC cân tại E

d) EC = ED

Mà AC = BD (ABCD là hình thang cân)

⇒ EA = EB

Lại có OA = OB

⇒ OE là đường trung trực AB

OD = OC; EC = ED

⇒ OE là đường trung trực CD.

Câu 2

Cho ∆ABC có a = 7, b = 8, c = 5. Tính số đo góc A, diện tích S của tam giác ABC, đường cao kẻ từ đỉnh A là h_a và bán kính R của đường tròn ngoại tiếp tam giác ABC.

Xem đáp án

Lời giải

Lời giải:

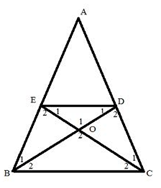
Media VietJack

Theo hệ quả của định lí côsin ta có:

\[\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{8^2} + {5^2} - {7^2}}}{{2.8.5}} = \frac{1}{2}\]

\( \Rightarrow \widehat A = 60^\circ \).

Diện tích tam giác ABC là \(S = \frac{1}{2}bc\sin A = \frac{1}{2}.8.5.\sin 60^\circ = 10\sqrt 3 \).

Vì \(S = \frac{1}{2}a{h_a}\) nên \({h_a} = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{7} = \frac{{20\sqrt 3 }}{7}\)

Lại có: \(S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{7.8.5}}{{4.10\sqrt 3 }} = \frac{{7\sqrt 3 }}{3}\).

Câu 3