Phương trình \(\sin \left( {2x + \frac{\pi }{7}} \right) = {m^2} - 3m + 3\) vô nghiệm khi:
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
Đáp án đúng là: C
Ta có \( - 1 \le \sin \left( {2x + \frac{\pi }{7}} \right) \le 1,\,\,\forall x \in \mathbb{R}\).
Phương trình \(\sin \left( {2x + \frac{\pi }{7}} \right) = {m^2} - 3m + 3\) vô nghiệm \( \Leftrightarrow \left[ \begin{array}{l}{m^2} - 3m + 3 > 1\\{m^2} - 3m + 3 < - 1\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{m^2} - 3m + 2 > 0\\{m^2} - 3m + 4 < 0\,\,\,\left( {vo\,\,nghiem} \right)\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}m < 1\\m > 2\end{array} \right.\)
Vậy \(\left[ \begin{array}{l}m < 1\\m > 2\end{array} \right.\) thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
– Lấy nước đổ vào đầy cái cốc loại 250 ml, sau đó đổ hết vào cái cốc loại 400 ml.
– Tiếp tục lấy nước đổ vào đầy cái cốc loại 250 ml, sau đó đổ vào cái cốc loại 400 ml cho đến khi cái cốc loại 400 ml chứa đầy nước.
– Khi đó trong cái cốc loại 250 ml còn lại 100 ml nước.
Lời giải
Lời giải
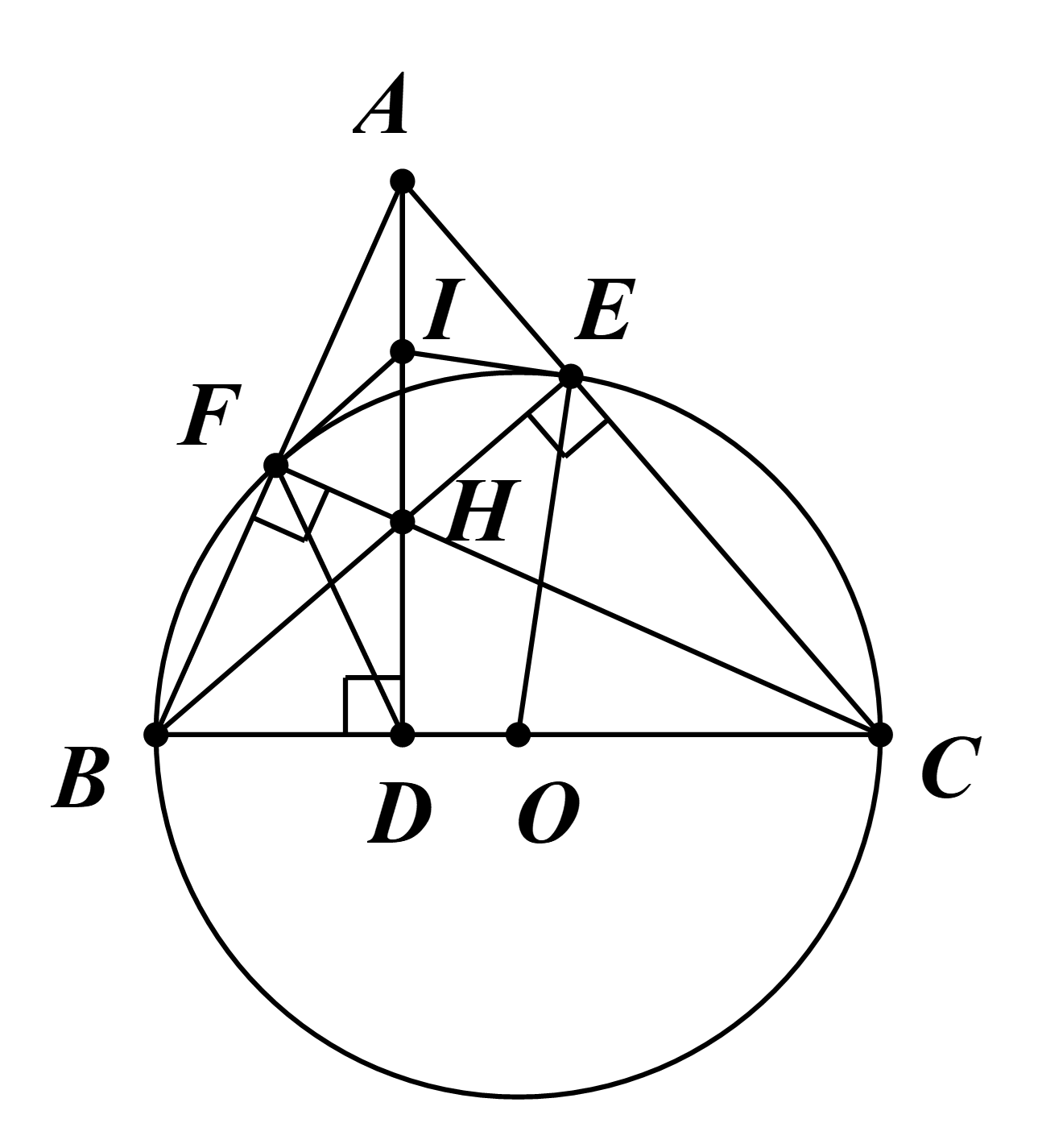
a) ∆BCF nội tiếp đường tròn tâm O, đường kính BC.
Suy ra \(\widehat {BFC}\) là góc nội tiếp chắn nửa đường tròn đường kính BC.
Khi đó \(\widehat {BFC} = 90^\circ \) hay \(\widehat {AFH} = 90^\circ \).
Vì vậy ba điểm A, F, H cùng thuộc đường tròn đường kính AH (1)
Chứng minh tương tự, ta được \(\widehat {AEH} = 90^\circ \).
Suy ra ba điểm A, E, H cùng thuộc đường tròn đường kính AH (2)
Từ (1), (2), ta được tứ giác AEHF nội tiếp đường tròn đường kính AH.
b) Ta có \(\widehat {FIE} = 2\widehat {FAE} = 2.60^\circ = 120^\circ \) (góc nội tiếp bằng một nửa số đo của của bị chắn).
Suy ra .
Ta có I là tâm đường tròn ngoại tiếp tứ giác AEHF (giả thiết).
Suy ra I là trung điểm AH.
Do đó \(IA = IH = \frac{{AH}}{2} = \frac{4}{2} = 2\,\,\left( {cm} \right)\).
Diện tích hình quạt IEHF của đường tròn (I) là:
\(S = \frac{{\pi .I{A^2}.n^\circ }}{{360^\circ }} = \frac{{\pi {{.2}^2}.120^\circ }}{{360^\circ }} = \frac{{4\pi }}{3}\,\,\,\left( {c{m^2}} \right)\).
Vậy sđ và diện tích hình quạt IEHF của đường tròn (I) bằng \(\frac{{4\pi }}{3}\,\,c{m^2}\).
c) ∆ABC có hai đường cao CF và BE cắt nhau tại H.
Suy ra H là trực tâm của ∆ABC.
Mà AH cắt BC tại D.
Do đó AD ⊥ BC.
Suy ra \(\widehat {HDB} = 90^\circ \).
Khi đó ba điểm B, D, H cùng thuộc đường tròn đường kính BH (3)
Lại có \(\widehat {BFH} = 90^\circ \) (chứng minh trên).
Suy ra ba điểm B, F, H cùng thuộc đường tròn đường kính BH (4)
Từ (3), (4), suy ra tứ giác BDHF nội tiếp đường tròn đường kính BH.
Do đó \(\widehat {HFD} = \widehat {HBD}\) (cùng chắn ) (*)
Ta có tứ giác AEHF nội tiếp đường tròn đường kính AH (chứng minh trên).
Suy ra \(\widehat {EFH} = \widehat {EAH}\) (cùng chắn ) (**)
Ta có \(\widehat {EBC} = \widehat {CAD}\) (cùng phụ với \(\widehat {ACB}\)) (***)
Từ (*), (**), (***), suy ra \(\widehat {HFD} = \widehat {EFH}\).
Vậy FH là tia phân giác của \(\widehat {DFE}\).
d) Ta có tứ giác AEHF nội tiếp đường tròn đường kính AH (chứng minh trên).
Suy ra IE = IH.
Do đó ∆IEH cân tại I.
Vì vậy \(\widehat {IEH} = \widehat {IHE}\) (5)
Lại có \(\widehat {BHD} = \widehat {IHE}\) (cặp góc đối đỉnh) (6)
Mà \(\widehat {BHD} = \widehat {ECO}\) (cùng phụ với \(\widehat {ABC}\)) (7)
Ta có tứ giác BCEF nội tiếp đường tròn tâm O, đường kính BC (giả thiết).
Suy ra OE = OC.
Do đó ∆OEC cân tại O.
Vì vậy \(\widehat {ECO} = \widehat {OEC}\) (8)
Từ (5), (6), (7), (8), suy ra \(\widehat {IEH} = \widehat {OEC}\).
Mà \(\widehat {OEH} + \widehat {OEC} = 90^\circ \) (do BE ⊥ AC).
Suy ra \(\widehat {OEH} + \widehat {IEH} = 90^\circ \).
Do đó \(\widehat {IEO} = 90^\circ \).
Vì vậy OE ⊥ EI.
Suy ra IE là tiếp tuyến của (O).
Chứng minh tương tự, ta được IF là tiếp tuyến của (O).
Mà I ∈ AH.
Vậy 2 tiếp tuyến của (O) tại E, F và AH đồng quy tại điểm I.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.