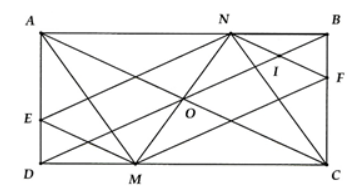
Cho hình chữ nhật ABCD, O là giao điểm hai đường chéo. M thuộc CD và N thuộc AB sao cho DM = BN.
a) Chứng minh ANCM là hình bình hành, từ đó suy ra các điểm M, O, N thẳng hàng.
b) Qua M kẻ đuờng thẳng song song với AC cắt AD ở E, qua N kẻ đường thẳng song song với AC cắt BC ở F. Chứng minh tứ giác ENFM là hình bình hành.
c) Tìm vị trí của điểm M, N để ANCM là hình thoi.
d) BD cắt NF tại I. Chứng minh I là trung điểm của NF
Cho hình chữ nhật ABCD, O là giao điểm hai đường chéo. M thuộc CD và N thuộc AB sao cho DM = BN.
a) Chứng minh ANCM là hình bình hành, từ đó suy ra các điểm M, O, N thẳng hàng.
b) Qua M kẻ đuờng thẳng song song với AC cắt AD ở E, qua N kẻ đường thẳng song song với AC cắt BC ở F. Chứng minh tứ giác ENFM là hình bình hành.
c) Tìm vị trí của điểm M, N để ANCM là hình thoi.
d) BD cắt NF tại I. Chứng minh I là trung điểm của NF
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
a) Ta chứng minh \[\left\{ \begin{array}{l}AN = CM\\AN\parallel CM\end{array} \right. \Rightarrow AMCN\] là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
\( \Rightarrow \) O là trung điểm MN
b) Ta có: EM // AC nên \(\widehat {EMD} = \widehat {ACD}\) (2 góc so le trong)
NF // AC nên \(\widehat {BNF} = \widehat {BAC}\) (2 góc so le trong)
Mà \(\widehat {BAC} = \widehat {ACD}\) (vì AB // DC, tính chất hình chữ nhật)
\( \Rightarrow \widehat {EMD} = \widehat {BNF}\)
Từ đó chứng minh được: ∆EDM = ∆FBN (g.c.g)
\( \Rightarrow \)EM = FN
Lại có EM // FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
c) Tứ giác ANCM là hình thoi \( \Leftrightarrow AC \bot MN\) tại O \( \Rightarrow \) M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O \( \Rightarrow \widehat {OCB} = \widehat {OBC}\) và \(\widehat {NFB} = \widehat {OCF}\)(đv)
\( \Rightarrow \) \(\Delta \)BFI cân tại I
\( \Rightarrow \) IB = IF (1)
Ta lại chứng minh được ∆NIB cân tại I \( \Rightarrow \) IN = IB (2)
Từ (1) và (2) \( \Rightarrow \) I là trung điểm của NF.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Diện tích xung quanh căn phòng đó là:
(4,5 + 3,5) × 2 × 4 = 64 (m2)
Diện tích trần của căn phòng đó là:
4,5 × 3,5 = 15,75 (m2)
Diện tích cần quét vôi của căn phòng đó là:
64 + 15,75 – 7,8 = 71,95 (m2)
Đáp số: 71,95 m2.
Lời giải
Lời giải
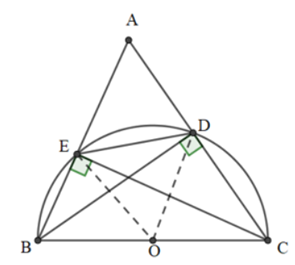
a) Gọi O là trung điểm của BC
\( \Rightarrow OB = OC = \frac{1}{2}BC\) (1)
Xét tam giác DBC vuông tại D (do DB là đường cao của tam giác ABC)
Có DO là đường trung tuyến ứng với cạnh huyền BC
\( \Rightarrow OD = \frac{1}{2}BC\) (2) (tính chất đường trung tuyến ứng với cạnh huyền)
Từ (1) và (2) suy ra \(OB = OC = OD = \frac{1}{2}BC\).
Do đó, ba điểm B, C, D cùng nằm trên đường tròn tâm O bán kính OB.
Xét tam giác BEC vuông tại E (do CE là đường cao của tam giác ABC)
Có EO là đường trung tuyến ứng với cạnh huyền BC
\(OE = \frac{1}{2}BC\) (3) (tính chất đường trung tuyến ứng với cạnh huyền)
Từ (1) và (3) suy ra \(OB = OC = OE = \frac{1}{2}BC\).
Do đó, ba điểm B, C, E cùng nằm trên đường tròn tâm O bán kính OB.
Do đó, bốn điểm B, C, E, D cùng nằm trên một đường tròn tâm O bán kính OB.
b) Xét đường tròn tâm O bán kính OB có đường kính BC.
Ta có DE là một dây cung không đi qua tâm O nên BC > DE do trong một đường tròn dây cung lớn nhất là đường kính.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.