Câu hỏi:
30/05/2023 118Cho tam giác ABC. Các đường cao AD, BE, CK (D, E, K tương ứng thuộc các cạnh BC, CA, AB) gọi là các đường n – tuyến của DABC nếu như: \[\frac{{BD}}{{BC}} = \frac{{CE}}{{CA}} = \frac{{AK}}{{AB}} = \frac{1}{n}\](n là số dương cho trước). Đặt AD = da, BE = db, CK = dc (và gọi da, db, dc là độ dài của các đường n - tuyến). Chứng minh rằng:
da2 + db2 + dc2 = \[\frac{{{n^2} - n + 1}}{n}\left( {{a^2} + {b^2} + {c^2}} \right)\].
Sách mới 2k7: 30 đề đánh giá năng lực DHQG Hà Nội, Tp. Hồ Chí Minh, BKHN 2025 mới nhất (600 trang - chỉ từ 160k).
Quảng cáo
Trả lời:
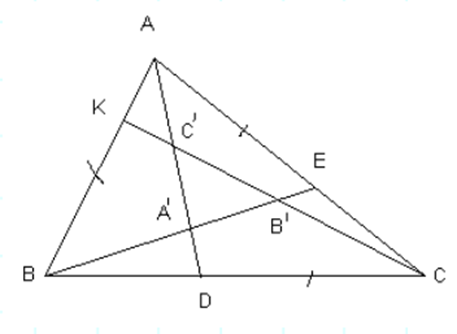
Theo định lý Steward ta có:
a.AD2 = BD.b2 - DC.c2 - a.BD.DC (1)
Do \[BD = \frac{a}{n},DC = \frac{{\left( {n - 1} \right)a}}{n}\], vậy từ (1) có:
a.AD2 = \[\frac{{a{b^2}}}{n} + \frac{{\left( {n - 1} \right)a{c^2}}}{n} - a.\frac{{a\left( {n - 1} \right)a}}{{{n^2}}}\]
\[ \Rightarrow {d_a}^2 = \frac{{{b^2} + \left( {n - 1} \right)a{c^2}}}{n} - \frac{{\left( {n - 1} \right){a^2}}}{{{n^2}}}\]
\[ \Rightarrow {d_a}^2 = \frac{{n{b^2} + n\left( {n - 1} \right){c^2} - \left( {n - 1} \right){a^2}}}{{{n^2}}}\] (2)
Lý luận tương tự, ta có: \[{d_b}^2 = \frac{{n{c^2} + n\left( {n - 1} \right){a^2} - \left( {n - 1} \right){b^2}}}{{{n^2}}}\] (3)
\[{d_c}^2 = \frac{{n{a^2} + n\left( {n - 1} \right){b^2} - \left( {n - 1} \right){c^2}}}{{{n^2}}}\] (4)
Cộng từng vế (2), (3), (4) suy ra:
\[{d_a}^2 + {d_b}^2 + {d_c}^2 = \frac{{{n^2} - n + 1}}{{{n^2}}}\left( {{a^2} + {b^2} + {c^2}} \right)\](đpcm)
Vậy \[{d_a}^2 + {d_b}^2 + {d_c}^2 = \frac{{{n^2} - n + 1}}{{{n^2}}}\left( {{a^2} + {b^2} + {c^2}} \right)\].
Đã bán 152
Đã bán 114
Đã bán 132
Đã bán 47
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho tam giác ABC, D là trung điểm của AC, E là trung điểm của AB. Trên tia đối của DB lấy điểm N sao cho DN = DB. Trên tia đối của tia EC lấy điểm M sao cho EM = EC. Chứng minh rằng A là trung điểm của MN.
Câu 4:
Một căn phòng hình chữ nhật có chiều dài 8 m, chiều rộng 6 m. Người ta dùng các viên gạch men hình vuông cạnh 4 dm để lát nền căn phòng đó. Hỏi:
a) Hỏi cần bao nhiêu viên gạch men để lát kín nền căn phòng đó? (Phần diện tích mạch vữa không đáng kể).
b) Biết giá tiền 1m2 gạch men loại đó là 120 000 đồng. Hỏi phải tốn bao nhiêu tiền mua gạch men để lát kín nền căn phòng đó?
Câu 5:
Khi chia số tự nhiên a cho 54, ta được số dư là 38. Khi chia a cho 18 ta được thương là 14 và còn dư. Tìm số a.
Câu 6:
Một hình chữ nhật có chu vi là 24 cm, chiều dài gấp 3 lần chiều rộng. Tìm diện tích của hình chữ nhật đó?
Câu 7:
Cho 2 đường thẳng xx' và yy' song song với nhau. Đường thẳng a cắt xx', yy' lần lượt tại A và B. Tia At là tia phân giác của \[\widehat {xAB}\].
a) Chứng minh tia At cắt đường thẳng yy'.
b) Cho \[\widehat {xAB} = 70^\circ \], At cắt yy' tại C. Tính số đo góc ACB.
về câu hỏi!