Câu hỏi:
13/07/2024 406
Cho 2 đường thẳng xx' và yy' song song với nhau, một đường thẳng cắt xx' và yy' lần lượt tại các điểm A, A'. Kẻ tia phân giác Az của \[\widehat {x'AA'}\] và tia phân giác A't của \[\widehat {yA'A}\]. Tia Az cắt yy' tại điểm B' và A't cắt xx' tại điểm B.
a) Chứng tỏ Az // A't.
b) Chứng tỏ \[\widehat {ABA'} = \widehat {AB'A'}\].
Cho 2 đường thẳng xx' và yy' song song với nhau, một đường thẳng cắt xx' và yy' lần lượt tại các điểm A, A'. Kẻ tia phân giác Az của \[\widehat {x'AA'}\] và tia phân giác A't của \[\widehat {yA'A}\]. Tia Az cắt yy' tại điểm B' và A't cắt xx' tại điểm B.
a) Chứng tỏ Az // A't.
b) Chứng tỏ \[\widehat {ABA'} = \widehat {AB'A'}\].
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
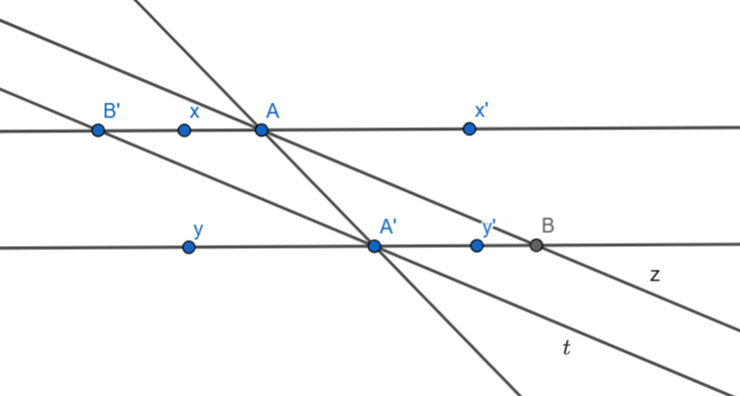
a) Xét DB'AA' và DAA'B có:
AA' là cạnh chung
\[\widehat {B'{\rm{AA}}'} = \widehat {AA'B}\] (gt)
B'A = A'B (gt)
Do đó DB'AA' = DAA'B (c.g.c)
Suy ra \[\widehat {B'A'A} = \widehat {BAA'}\] (hai góc tương ứng)
Do đó Az // A't (đpcm)
b) Ta có DB'AA' = DAA'B (cmt)
Suy ra \[\widehat {AB'A'} = \widehat {ABA'}\](đpcm)
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một căn phòng hình chữ nhật có chiều dài 8 m, chiều rộng 6 m. Người ta dùng các viên gạch men hình vuông cạnh 4 dm để lát nền căn phòng đó. Hỏi:
a) Hỏi cần bao nhiêu viên gạch men để lát kín nền căn phòng đó? (Phần diện tích mạch vữa không đáng kể).
b) Biết giá tiền 1m2 gạch men loại đó là 120 000 đồng. Hỏi phải tốn bao nhiêu tiền mua gạch men để lát kín nền căn phòng đó?
Một căn phòng hình chữ nhật có chiều dài 8 m, chiều rộng 6 m. Người ta dùng các viên gạch men hình vuông cạnh 4 dm để lát nền căn phòng đó. Hỏi:
a) Hỏi cần bao nhiêu viên gạch men để lát kín nền căn phòng đó? (Phần diện tích mạch vữa không đáng kể).
b) Biết giá tiền 1m2 gạch men loại đó là 120 000 đồng. Hỏi phải tốn bao nhiêu tiền mua gạch men để lát kín nền căn phòng đó?
Xem đáp án »
13/07/2024
12,515
Câu 3:
Cho tam giác ABC, D là trung điểm của AC, E là trung điểm của AB. Trên tia đối của DB lấy điểm N sao cho DN = DB. Trên tia đối của tia EC lấy điểm M sao cho EM = EC. Chứng minh rằng A là trung điểm của MN.
Cho tam giác ABC, D là trung điểm của AC, E là trung điểm của AB. Trên tia đối của DB lấy điểm N sao cho DN = DB. Trên tia đối của tia EC lấy điểm M sao cho EM = EC. Chứng minh rằng A là trung điểm của MN.
Xem đáp án »
13/07/2024
9,938
Câu 5:
Cho đường tròn (O; R) và dây\[AB = \frac{8}{5}R\]. Vẽ một tiếp tuyến song song vói AB, cắt các tia OA, OB lần lượt tại M và N. Tính diện tích tam giác OMN.
Cho đường tròn (O; R) và dây\[AB = \frac{8}{5}R\]. Vẽ một tiếp tuyến song song vói AB, cắt các tia OA, OB lần lượt tại M và N. Tính diện tích tam giác OMN.
Xem đáp án »
13/07/2024
4,051
Câu 6:
Một hình chữ nhật có chu vi là 24 cm, chiều dài gấp 3 lần chiều rộng. Tìm diện tích của hình chữ nhật đó?
Một hình chữ nhật có chu vi là 24 cm, chiều dài gấp 3 lần chiều rộng. Tìm diện tích của hình chữ nhật đó?
Xem đáp án »
13/07/2024
4,036
Câu 7:
12 người làm xong một công việc trong 4 ngày. Hỏi 16 người làm xong công việc đó trong bao nhiêu ngày ? (Mức làm của mỗi người như nhau).
12 người làm xong một công việc trong 4 ngày. Hỏi 16 người làm xong công việc đó trong bao nhiêu ngày ? (Mức làm của mỗi người như nhau).
Xem đáp án »
13/07/2024
3,694
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận