Câu hỏi:
13/07/2024 1,163
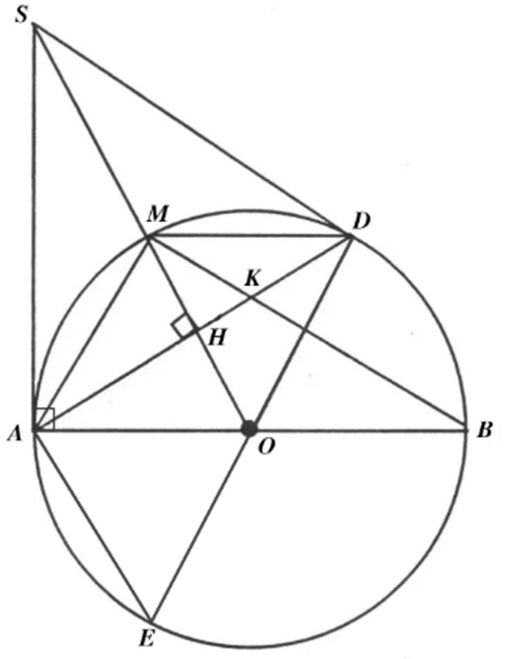
Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AM < MB. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn (O) tại D.
1. Chứng minh SD là tiếp tuyến của đường tròn (O).
2. Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính độ dài đoạn thẳng AE theo R và r.
3. Cho AM = r. Gọi K là giao điểm của BM và AD. Chứng minh: \(\frac{{M{D^2}}}{6} = KH.KD\).
Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AM < MB. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn (O) tại D.
1. Chứng minh SD là tiếp tuyến của đường tròn (O).
2. Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính độ dài đoạn thẳng AE theo R và r.
3. Cho AM = r. Gọi K là giao điểm của BM và AD. Chứng minh: \(\frac{{M{D^2}}}{6} = KH.KD\).
Câu hỏi trong đề:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
1.
Xét tam giác OAB có:
OA = OD = R
OH vuông góc với AD
Do đó, tam giác OAD cân tại O có OH là đường cao
Do đó, OH là phân giác của góc \(\widehat {AOD}\)
\( \Rightarrow \widehat {SOA} = \widehat {SOD}\)
Xét tam giác SAO và tam giác SDO có:
KO chung
\(\widehat {SOA} = \widehat {SOD}\)
OA = OD = R
Do đó, tam giác SAO bằng tam giác SDO (c.g.c)
\( \Rightarrow \widehat {SDO} = \widehat {SAO} = 90^\circ \)
Hay SD vuông góc với OD
Do đó, SD là tiếp tuyến của (O) tại D.
2,
Xét tam giác OAM có OA = OM
Do đó, tam giác OAM cân tại O
\( \Rightarrow \widehat {OAM} = \widehat {AMH}\)
Mà \(\widehat {OAM} + \widehat {SAM} = \widehat {SAO} = 90^\circ \)
Và \(\widehat {AMH} + \widehat {HAM} = 90^\circ \)
\( \Rightarrow \widehat {SAM} = \widehat {HAM}\)
Do đó, AM là đường phân giác của tam giác SAD (1)
Mặt khác SA, SD là các tiếp tuyến của đường tròn (O)
Do đó, SO là tia phân giác của \(\widehat {ASD}\)(2)
Từ (1) và (2) ta có: M là tâm đường tròn nội tiếp tam giác SAD.
Mà MH vuông góc với AD tại H nên MH là bán kính đường tròn nội tiếp tam giác SAD.
Do đó, MH = r, OH = R – r
Xét tam giác AOH vuông tại H
Ta có: OA2 = OH2 + AH2 (định lý Py–ta–go)
\( \Rightarrow AH = \sqrt {{R^2} - {{\left( {R - r} \right)}^2}} \Rightarrow AD = 2\sqrt {{R^2} - {{\left( {R - r} \right)}^2}} \)
Ta có: \(\widehat {EAD}\) chắn đường kính DE \( \Rightarrow \widehat {EAD} = 90^\circ \)
Xét tam giác EAD vuông tại A có:
DE2 = AD2 + AE2 (định lý Py–ta–go)
\( \Rightarrow AE = \sqrt {4{{\left( {R - r} \right)}^2}} = 2\left( {R - r} \right)\).
3.
OH là đường trung trực của AD, M thuộc OH
Do đó, DM = AM = R
Tứ giác AMDO có AM = MD = OA = OD (= R)
Tứ giác AMDO là hình thoi
Do đó, AM song song với DO.
Mà AM vuông góc với BM , BM vuông góc với OD
Tam giác OMD có OM = OD = CD (= R)
Do đó, tam giác OMD đều
Mà MB, DM là hai đường cao cắt nhau tại K của tam giác OMD
Do đó, K là trực tâm của tam giác đều OMD
Do đó, K là trọng tâm của tam giác đều OMD
\(KH = \frac{1}{3}DH;KD = \frac{2}{3}DH \Rightarrow KH.KD = \frac{2}{9}D{H^2}\)
Mà tam giác HMD vuông tại H
Do đó, DH = \(DH = MD.\sin 60^\circ = \frac{{\sqrt 3 }}{2}MD \Rightarrow MD = \frac{2}{{\sqrt 3 }}DH\)
\( \Rightarrow M{D^2} = 6.\frac{2}{9}D{H^2} = 6.KH.KD \Rightarrow \frac{{M{D^2}}}{6} = KH.KD\).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho biểu thức P = \(\left( {\frac{{{x^2}}}{{{x^3} - 4x}} + \frac{6}{{6 - 3x}} + \frac{1}{{x + 2}}} \right):\left( {x - 2 + \frac{{10 - {x^2}}}{{x + 2}}} \right)\).
a) Rút gọn P.
b) Tính giá trị của biểu thức P khi \(\left| x \right| = \frac{3}{4}\).
c) Với giá trị nào của x thì P = 7.
d) Tìm giá trị nguyên của x để P có giá trị nguyên.
Cho biểu thức P = \(\left( {\frac{{{x^2}}}{{{x^3} - 4x}} + \frac{6}{{6 - 3x}} + \frac{1}{{x + 2}}} \right):\left( {x - 2 + \frac{{10 - {x^2}}}{{x + 2}}} \right)\).
a) Rút gọn P.
b) Tính giá trị của biểu thức P khi \(\left| x \right| = \frac{3}{4}\).
c) Với giá trị nào của x thì P = 7.
d) Tìm giá trị nguyên của x để P có giá trị nguyên.
Xem đáp án »
13/07/2024
9,437
Câu 3:
8 người sơn được 3 cái nhà trong 6 giờ. Hỏi với 12 người sẽ sơn được bao nhiêu cái nhà trong 12 giờ ?
8 người sơn được 3 cái nhà trong 6 giờ. Hỏi với 12 người sẽ sơn được bao nhiêu cái nhà trong 12 giờ ?
Xem đáp án »
13/07/2024
7,107
Câu 5:
Cho hình vuông ABCD, O là giao điểm hai đường chéo AC và BD. Gọi M và N lần lượt là trung điểm của OB và CD.
a) CMR: \(\widehat {AMN} = 90^\circ \). Từ đó suy ra bốn điểm A, M, N, D cùng thuộc một đường tròn.
b) So sánh AN và MD.
Cho hình vuông ABCD, O là giao điểm hai đường chéo AC và BD. Gọi M và N lần lượt là trung điểm của OB và CD.
a) CMR: \(\widehat {AMN} = 90^\circ \). Từ đó suy ra bốn điểm A, M, N, D cùng thuộc một đường tròn.
b) So sánh AN và MD.
Xem đáp án »
13/07/2024
4,967
Câu 6:
Tổng của hai số lẻ bằng 64. Tìm 2 số đó,biết rằng giữa chúng có 5 số chẵn liên tiếp.
Tổng của hai số lẻ bằng 64. Tìm 2 số đó,biết rằng giữa chúng có 5 số chẵn liên tiếp.
Xem đáp án »
13/07/2024
3,792
Câu 7:
Lãi suất tiết kiệm có kì hạn của một ngân hàng là 0,6%. Bác Minh gửi 60000000 đồng tiền tiết kiệm, hỏi sau một tháng bác Minh có bao nhiêu tiền cả tiền vốn và lãi ?
Lãi suất tiết kiệm có kì hạn của một ngân hàng là 0,6%. Bác Minh gửi 60000000 đồng tiền tiết kiệm, hỏi sau một tháng bác Minh có bao nhiêu tiền cả tiền vốn và lãi ?
Xem đáp án »
13/07/2024
3,005
về câu hỏi!