Câu hỏi:

11/07/2024 899

Cho đường tròn (O) và dây cung AB của (O) không là đường kính. Gọi I là trung điểm của AB. Một đường thẳng thay đổi đi qua A cắt đường tròn tâm O bán kính OI tại P và Q.

a) Chứng minh rằng AP . AQ = AI².

b) Giả sử đường tròn ngoại tiếp tam giác BPQ cắt AB tại K khác B. Chứng minh
rằng AK . AB = AP . AQ.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

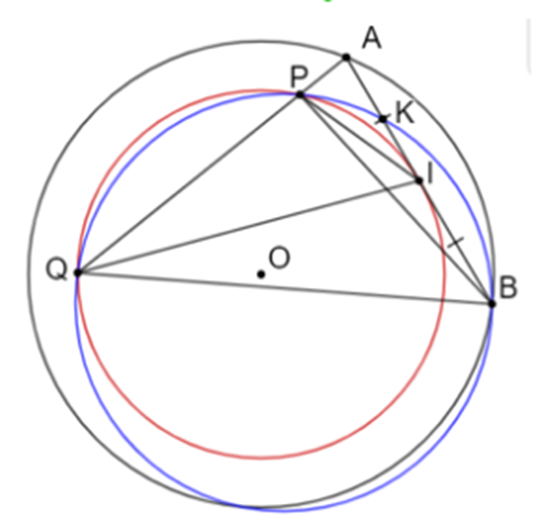
Cho đường tròn (O) và dây cung AB của (O) không là đường kính. Gọi I là trung điểm của (ảnh 1)

a) Xét (O; OA) có: \[IA = IB = \frac{1}{2}AB\]

⇒ OI ⊥ AB (mối quan hệ đường kính – dây cung)

⇒ OI ⊥ AI

Xét (O; OI) có: OI ⊥ AI

⇒ AI là tiếp tuyến của (O; OI) tại I

\[ \Rightarrow \widehat {PIA} = \widehat {PQI}\] (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn )

Hay \[\widehat {PIA} = \widehat {IQA}\]

Xét ∆AIP và ∆AQI có:

\[\widehat {PIA} = \widehat {IQA}\] (cmt)

\[\widehat A\] chung

Do đó ∆AIP ᔕ ∆AQI (g.g)

Suy ra \[\frac{{AI}}{{AQ}} = \frac{{AP}}{{AI}}\] (hai cạnh tương ứng tỉ lệ)

Do đó AP. AQ = AI².

b) Vì tứ giác BKPQ nội tiếp nên \[\widehat {APK} = \widehat {KBQ}\]

Hay \[\widehat {APK} = \widehat {ABQ}\]

Xét ∆APK và ∆ABQ có:

\[\widehat {APK} = \widehat {ABQ}\] (cmt)

\[\widehat A\]: góc chung

Do đó ∆APK ᔕ ∆ABQ (g. g)

Suy ra \[\frac{{AP}}{{AB}} = \frac{{AK}}{{AQ}}\] (hai cạnh tương ứng tỉ lệ)

Do đó AK . AB = AP . AQ.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một vận động viên bắn súng, bắn ba viên đạn. Xác suất để trúng cả ba viên vòng 10 là 0,0008; xác suất đề một viên trúng vòng 8 là 0,15; xác suất để một viên trúng vòng dưới 8 là 0,4. Biết rằng các lần bắn là độc lập với nhau. Xác suất để vận động viên đó đạt ít nhất 28 điểm có giá trị gần bằng nhất với số nào sau đây?

A. 0,0494;

B. 0,0981;

C. 0,0170;

D. 0,0332.

Lời giải

Đáp án đúng là: A

Xác suất để một viên trúng vòng 10 là: \[\sqrt[3]{{0,008}} \approx 0,0928\].

Xác suất để một viên trúng vòng 9 là:

1 − 0,4 − 0,0928 − 0,15 = 0,3572.

Các trường hợp xảy ra để thỏa mãn yêu cầu bài toán:

* Điểm ba lần bắn là 28 điểm, có 2 trường hợp: hai viên vòng 9 và một viên vòng 10 hoặc hai viên vòng 10 và một viên vòng 8.

Xác suất trong trường hợp này bằng:

\[\mathop P\nolimits_1 = C_3^2\,\,.\,\,{(0,3572)^2}\,.\,\,0,0928 + C_3^2\,\,.\,\,{(0,0928)^2}\,.\,\,0,15 \approx 0,0394\].

* Điểm ba lần bắn là 29 điểm, có 1 trường hợp: hai viên vòng 10 và một viên vòng 9. Xác suất trường hợp này bằng:

\[{P_2} = C_3^2\,\,.\,{(0,0928)^2}\,.\,\,0,3572 \approx 0,0092\].

* Điểm ba lần bắn là 30 điểm, có 1 trường hợp là cả ba viên vòng 10: Xác suất bằng 0,0008.

Vậy xác suất cần tìm bằng: P₁ + P₂ + 0,0008 = 0,00494.

Câu 2

Một đơn vị bộ đội chuẩn bị một số gạo đủ cho 50 người ăn trong 10 ngày, 3 ngày sau được tăng thêm 20 người. Hỏi đơn vị cần chuẩn bị bao nhiêu suất gạo nữa để cả đơn vị đủ ăn trong những ngày sau đó? (Số gạo mỗi người ăn trong một ngày là một suất gạo)

Xem đáp án

Lời giải

Số gạo đó đủ cho số người ăn trong 1 ngày là:

50 . 10 = 500 (người)

Số gạo đã ăn đủ cho số người ăn trong 1 ngày là:

50 . 3 = 150 (người)

Số gạo còn lại đủ cho số người ăn trong 1 ngày là:

500 – 150 = 350 (người)

Sau ngày thứ 3 thì có số người ăn là:

50 + 20 = 70 (người)

Số ngày còn lại là:

10 – 3 = 7 (ngày)

Số suất ăn cần là:

70 . 7 = 490 (suất)

Cần thêm số suất ăn là:

490 – 350 = 140 (suất)

Đáp số: 140 suất.

Câu 3