Câu hỏi:
11/07/2024 1,830
Cho ∆ABC có E là trung điểm của AC. Qua E kẻ ED // AB (D ∈ BC), EF // BC (F ∈ AB).
a) Chứng minh tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.
b) Gọi H là điểm đối xứng của D qua F. CHứng minh rằng HB // AD.
c) Gọi I là trung điểm của HB, K là giao điểm của AD và EF. Chứng minh rằng I, K, E thẳng hàng.
d) ∆ABC cần thêm điều kiện gì để HF = \[\frac{{AB}}{2}\].
Cho ∆ABC có E là trung điểm của AC. Qua E kẻ ED // AB (D ∈ BC), EF // BC (F ∈ AB).
a) Chứng minh tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.
b) Gọi H là điểm đối xứng của D qua F. CHứng minh rằng HB // AD.
c) Gọi I là trung điểm của HB, K là giao điểm của AD và EF. Chứng minh rằng I, K, E thẳng hàng.
d) ∆ABC cần thêm điều kiện gì để HF = \[\frac{{AB}}{2}\].
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
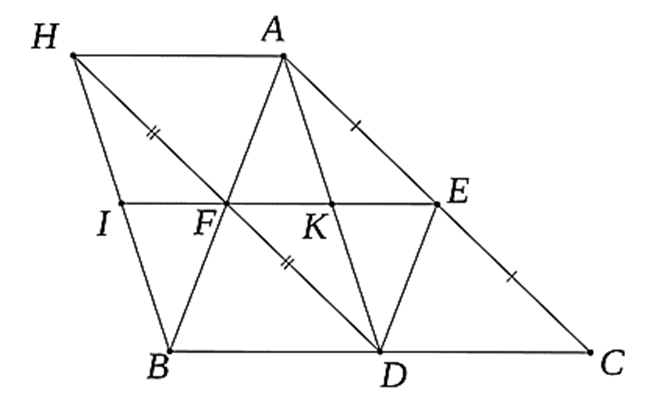
a)
Xét tứ giác BDEF có:
EF // BD (vì EF // BC)
ED // FB (vì ED // AB)
Do đó tứ giác BDEF là hình bình hành (tứ giác có cặp cạnh đối song song)
Tam giác ABC có:
EA = EC (gt)
ED // AB (gt)
Do đó DB = DC hay D là trung điểm của đoạn thẳng BC.
b)
Vì H đối xứng D qua F
⇒ F là trung điểm của HD (1)
Vì E là trung điểm của AC và EF // BC
⇒ F là trung điểm của AB (2)
Từ (1) và (2) ta có tứ giác HABD có hai đường chéo cắt nhau tại trung điểm mỗi đường.
⇒ AHBD là hình hình hành
⇒ HB // AD.
c)
Xét tam giác ∆HBD có:
I là trung điểm của HB
F trung điểm của HD
⇒ IF // BD (3)
Mà FE // BD (4)
⇒ I, F, E thẳng hàng.
⇒ I, K, E thẳng hàng.
d) Để HF = \(\frac{{AB}}{2}\) thì \(\frac{{HD}}{2} = \frac{{AB}}{2}\)
⇒ HD = AB
Hình bình hành AHBD có HD = AB
⇒ AHBD là hình chữ nhật
⇒ AD vuông góc với BC
Xét tam giác ABC có AD vừa là đường cao vừa là đường trung tuyến (D là trung điểm của BC)
⇒ ΔABC cân tại A.
Vậy ∆ABC cân tại A thì HF = \(\frac{{AB}}{2}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025)
Đã bán 1,1k
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Chứng minh rằng: tích của 3 số tự nhiên liên tiếp chia hết cho 3.
Xem đáp án »
11/07/2024
22,812
Câu 2:
Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên Oz lấy điểm I. Chứng minh:
a) Tam giác ∆AOI = tam giác ∆BOI.
b) AB vuông góc với OI.
Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên Oz lấy điểm I. Chứng minh:
a) Tam giác ∆AOI = tam giác ∆BOI.
b) AB vuông góc với OI.
Xem đáp án »
11/07/2024
15,872
Câu 3:
Cho \[A = \frac{1}{{1.2}} + \frac{1}{{3.4}} + \frac{1}{{5.6}} + .... + \frac{1}{{99.100}}\]. Chứng minh rằng: \(\frac{7}{{12}}\) < A < \(\frac{5}{6}\).
Cho \[A = \frac{1}{{1.2}} + \frac{1}{{3.4}} + \frac{1}{{5.6}} + .... + \frac{1}{{99.100}}\]. Chứng minh rằng: \(\frac{7}{{12}}\) < A < \(\frac{5}{6}\).
Xem đáp án »
11/07/2024
14,385
Câu 5:
Một bếp ăn dự trữ gạo cho 80 người ăn trong 30 ngày. Nay có thêm 40 người nữa mới đến. Hỏi số gạo đó đủ ăn trong bao nhiêu ngày?
Một bếp ăn dự trữ gạo cho 80 người ăn trong 30 ngày. Nay có thêm 40 người nữa mới đến. Hỏi số gạo đó đủ ăn trong bao nhiêu ngày?
Xem đáp án »
11/07/2024
5,481
Câu 6:
Lớp 10A có 45 học sinh trong kì thi học kì 1 có 25 em đạt loại giỏi môn toán, 20 em đạt loại giỏi môn lý, 18 em đạt loại giỏi môn hoá. 6 em ko đạt loại giỏi bất kì môn nào, 5 em đạt loại giỏi 3 môn. Hỏi số học sinh chỉ đạt giỏi một môn và số học sinh giỏi hai môn?
Lớp 10A có 45 học sinh trong kì thi học kì 1 có 25 em đạt loại giỏi môn toán, 20 em đạt loại giỏi môn lý, 18 em đạt loại giỏi môn hoá. 6 em ko đạt loại giỏi bất kì môn nào, 5 em đạt loại giỏi 3 môn. Hỏi số học sinh chỉ đạt giỏi một môn và số học sinh giỏi hai môn?
Xem đáp án »
11/07/2024
4,190
Câu 7:
Một bếp ăn dự trữ gạo đủ cho 120 người ăn trong 18 ngày. Nay có 80 người được chuyển đi nơi khác. Hỏi số gạo đó đủ cho những người còn lại ăn trong bao nhiêu ngày? (Mức ăn mỗi người như nhau).
Một bếp ăn dự trữ gạo đủ cho 120 người ăn trong 18 ngày. Nay có 80 người được chuyển đi nơi khác. Hỏi số gạo đó đủ cho những người còn lại ăn trong bao nhiêu ngày? (Mức ăn mỗi người như nhau).
Xem đáp án »
11/07/2024
4,038
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận