Câu hỏi:

11/07/2024 1,071

Cho tam giác ABC cân tại A. Trên tia đối của tia BC và tia đối của tia CB theo thứ tự lấy hai điểm D và E sao cho BD = CE.

Chứng minh ∆ADE cân.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

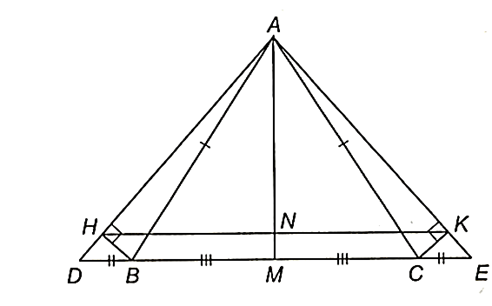
Cho tam giác ABC cân tại A. Trên tia đối của tia BC và tia đối của tia CB theo thứ tự lấy (ảnh 1)

Do ∆ABC cân tại A nên \[\widehat {ABC} = \widehat {ACB}\].

Suy ra \[\widehat {ABD} = \widehat {ACE}\](cùng bù với gióc \[\widehat {ABC},\widehat {ACB}\]).

Xét ∆ABD và ∆ACE có:

AB = AC (do tam giác ABC cân tại A)

\[\widehat {ABD} = \widehat {ACE}\] (chứng minh trên),

Mà BD = CE (theo giả thiết).

Suy ra ∆ABD = ∆ACE (c.g.c),

Do đó AD = AE (hai cạnh tương ứng),

Suy ra tam giác ADE cân tại A.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Chứng minh rằng: tích của 3 số tự nhiên liên tiếp chia hết cho 3.

Xem đáp án

Lời giải

Gọi tích của 3 số liên tiếp là:

A= a ∙ (a + 1) ∙ (a + 2) (a thuộc ℕ^*)

Giả sử a ⋮ 3 ⇒ A ⋮ 3

Nếu a ko chia hết cho 3 thì có 2 khả năng: 3n + 1 hoặc 3n + 2

Với a = 3n + 1

⇒ a + 2 = (3n + 1) + 2 = 3n + 3 ⋮ 3

⇒ A ⋮ 3 (1)

Với a = 3n + 2

⇒ a +1 = 3n + 2 + 1 = 3n + 3 ⋮ 3

⇒ A chia hết 3 (2)

Vậy với mọi A thuộc N thì A ⋮ 3 (điều đã được chứng minh).

Câu 2

Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên Oz lấy điểm I. Chứng minh:

a) Tam giác ∆AOI = tam giác ∆BOI.

b) AB vuông góc với OI.

Xem đáp án

Lời giải

Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox lấy điểm A, trên Oy lấy điểm B (ảnh 1)

Vì Oz là phân giác của xOy nên \[xOz = yOz = \frac{{xOy}}{2}\]

Xét Δ AOI và Δ BOI có:

OA = OB (gt)

AOI = BOI (cmt)

OI là cạnh chung

Do đó, Δ AOI = Δ BOI (c.g.c) (đpcm)

Xét Δ AOH và Δ BOH có:

OA = OB (gt)

AOH = BOH (câu a)

HO là cạnh chung.

Do đó, Δ AOH = Δ BOH (c.g.c)

⇒ AHO = BHO (2 góc tương ứng)

Mà AHO + BHO = 180° (kề bù) nên AHO = BHO = 90°

⇒ AB ⊥ OI (đpcm).

Câu 3