Câu hỏi:
07/06/2023 253
Trong mặt phẳng tọa độ, cho tam giác có ba đỉnh A(3; 4), B(5; 1), C(–1; – 2). Lập phương trình tham số của đường thẳng đi qua B và song song với AC.
Trong mặt phẳng tọa độ, cho tam giác có ba đỉnh A(3; 4), B(5; 1), C(–1; – 2). Lập phương trình tham số của đường thẳng đi qua B và song song với AC.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi đường thẳng đi qua B và song song với AC là d.
Ta có: d // AC nên \(\overrightarrow {{u_d}} = \overrightarrow {AC} \)= (–4; –6) = –2(2; 3)
Phương trình tham số của d là: \(\left\{ \begin{array}{l}x = 5 + 2t\\y = 1 + 3t\end{array} \right.\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Nếu Hòa cho Bình 10 viên bi thì số bi của hai bạn bằng nhau nên ban đầu Hoà hơn Bình số bi là:
2 . 10 = 20 (viên)
Số bi của Hoà ban đầu là:
(120 + 20) : 2 = 70 (viên)
Số bi của Bình ban đầu là:
70 – 20 = 50 (viên)
Đáp số: Hoà: 70 viên; Bình: 50 viên.
Lời giải
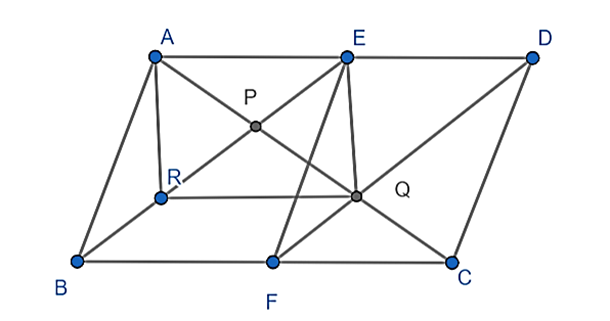
a) Ta có: ED = \(\frac{1}{2}AD\)
BF = \(\frac{1}{2}BC\)
Mà ABCD là hình bình hành nên AD = BC và AD// BC
Suy ra: ED = BF và ED // BF
Vậy EDFB là hình bình hành.
b) Vì EB // DF nên EP // DQ
Xét tam giác ADQ có:
EP // DQ và E là trung điểm AD nên PE là đường trung bình của tam giác ADQ.
Suy ra: P là trung điểm AQ hay AP = PQ (1)
Xét tam giác BPC có:
FQ // BP và F là trung điểm BC nên FQ là đường trung bình của tam giác BPC.
Suy ra: Q là trung điểm của PC hay PQ = QC (2)
Từ (1) và (2) suy ra: AP = PQ = QC.
c) Do AE // BC nên áp dụng định lí Thalès ta có:
\(\frac{{AP}}{{PC}} = \frac{{EP}}{{PB}} = \frac{1}{2}\)
Mặt khác R là trung điểm PB nên PR = RB = \(\frac{1}{2}PB\)
Suy ra: EP = PR = RB = \(\frac{1}{2}PB\)
Xét tứ giác ARQE có:
AP = PQ và PE = PR (2 đường chéo AQ, RE cắt nhau tại trung điểm mỗi đường)
Vậy tứ giác ARQE là hình bình hành.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận