Cho (O; R) và 3 dây AB, AC, AD; gọi M và N là lần lượt là hình chiếu của B trên các đường thẳng AC, AD. Chứng minh MN ≤ 2R

Quảng cáo

Trả lời:

Giải bởi Vietjack

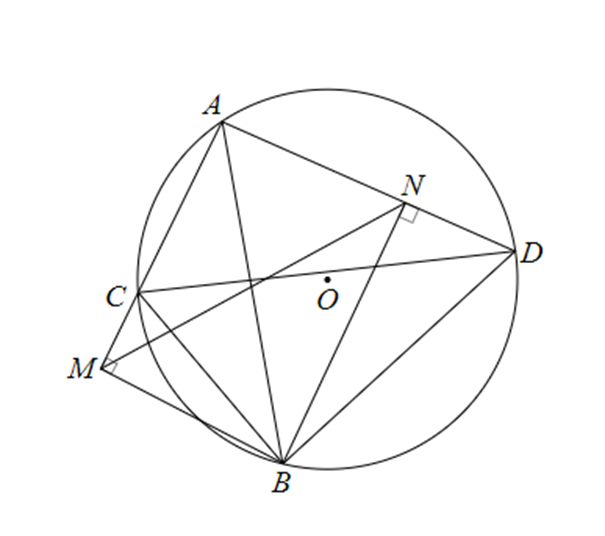
\[\widehat {BMC} = \widehat {BND} = 90^\circ ,\widehat {BCM} = \widehat {BDN}\]

∆BMC ᔕ ∆BND (g.g)

\[\frac{{BM}}{{BC}} = \frac{{BN}}{{BD}}\] và $\widehat {MBN} = \widehat {CDB}$

∆BMC ᔕ ∆BND (g.c.g)

\[\frac{{MN}}{{CD}} = \frac{{BN}}{{BD}} \le \frac{{BD}}{{BD}} = 1\]

MN ≤ CD

Ta thấy CD là một dây của đường tròn (O; R) nên CD ≤ 2R

Do đó MN ≤ 2R. Dấu “=” xảy ra khi và chỉ khi N trùng D và CD là đường kính của (O).

Tứ giác ABCD là hình chữ nhật. Từ đó suy ra vị trí của 3 dây AB, AC, AD.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Xem đáp án

Lời giải

Số học sinh học giỏi ít nhất 1 môn toán hoặc tiếng việt là:

40 – 2 = 38 (học sinh)

Nếu mỗi bạn chỉ thích 1 môn thì có tất cả số học sinh là:

30 + 25 = 55 (học sinh)

Vậy thì thừa ra số học sinh chính là số học sinh giỏi cả toán và tiếng việt là:

55 – 38 = 17 (học sinh)

Đáp số: 17 học sinh

Câu 2

Xem đáp án

Lời giải

Các số có hai chữ số ta viết thành dãy: 10, 11, 12, ..., 99

Số hạng của dãy là

(99 – 10) + 1 = 90 (số)

Trong dãy trên có 9 số có hai chữ số giống nhau là 11, 22, 33, 44, 55, 66, 77, 88, 99

Số có hai chữ số khác nhau là

90 – 9 = 81 (số)

Đáp số: 81 số.

Câu 3