Cho hình thang vuông ABCD tại A và D. Gọi E, F lần lượt là trung điểm của AD, BC. Chứng minh:
a) ∆AFD cân tại F.
b) \(\widehat {BAF} = \widehat {CDF}\).
Cho hình thang vuông ABCD tại A và D. Gọi E, F lần lượt là trung điểm của AD, BC. Chứng minh:
a) ∆AFD cân tại F.
b) \(\widehat {BAF} = \widehat {CDF}\).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
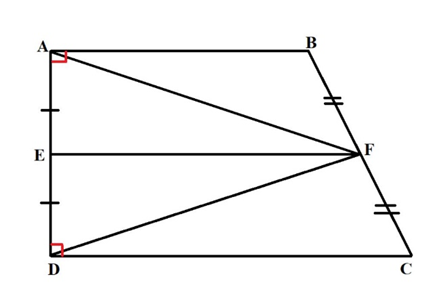
a) Ta có EF là đường trung bình của hình thang ABCD
⇒ EF // AB
Suy ra EF ⊥ AD.
Khi đó EF vừa là trung tuyến vừa là đường cao của tam giác AFD (đpcm)
Vậy tam giác AFD cân tại F.
b) Tam giác AFD cân tại F nên \(\widehat {EAF} = \widehat {EDF}\).
Suy ra \(\widehat {FAB} = \widehat {CDF}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số học sinh học giỏi ít nhất 1 môn toán hoặc tiếng việt là:
40 – 2 = 38 (học sinh)
Nếu mỗi bạn chỉ thích 1 môn thì có tất cả số học sinh là:
30 + 25 = 55 (học sinh)
Vậy thì thừa ra số học sinh chính là số học sinh giỏi cả toán và tiếng việt là:
55 – 38 = 17 (học sinh)
Đáp số: 17 học sinh
Lời giải
Các số có hai chữ số ta viết thành dãy: 10, 11, 12, ..., 99
Số hạng của dãy là
(99 – 10) + 1 = 90 (số)
Trong dãy trên có 9 số có hai chữ số giống nhau là 11, 22, 33, 44, 55, 66, 77, 88, 99
Số có hai chữ số khác nhau là
90 – 9 = 81 (số)
Đáp số: 81 số.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo