Câu hỏi:
04/07/2023 290
Cho đường tròn (O; R), đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax, kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao điểm của CO và AD là I. Chứng minh: CO ⊥ AD.
Cho đường tròn (O; R), đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax, kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao điểm của CO và AD là I. Chứng minh: CO ⊥ AD.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
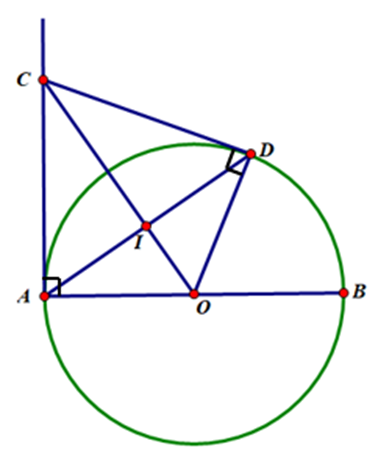
Ta có CA, CD là hai tiếp tuyến của (O) cắt nhau tại C.
Suy ra CA = CD.
Khi đó C nằm trên đường trung trực của đoạn thẳng AD (1)
Lại có OA = OD = R.
Suy ra O nằm trên đường trung trực của đoạn thẳng AD (2)
Từ (1), (2), suy ra CO là đường trung trực của đoạn thẳng AD.
Vậy CO ⊥ AD tại I.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chiều rộng là:
16 : 2 = 8 (m)
Diện tích mảnh đất là:
16 ´ 8=128 (m2)
Số hoa hồng cần trồng là:
128 : 4 = 32 (cây)
Đáp số: 32 cây
Lời giải
Gọi q(x); g(x) lần lượt là thương của phép chia f(x) cho x – 2; f(x) cho x2 – 1
Þ f(x) = q(x)(x– 2)
Và f(x) = g(x)(x2 – 1) + 2x
Þ f(2) = 8 + 4a + 2b + c = 0
f(1) = 1 + a + b + c = 2
f(–1) = – 1 + a – b + c = –2
Từ các hệ thức trên ta tìm được:
\[a = \frac{{10}}{3}\]; b = 1; \[c = \frac{{10}}{3}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)