Cho đường tròn (O; R) và điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) (E không trùng với D). Chọn câu đúng nhất:
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Đáp án đúng là: D
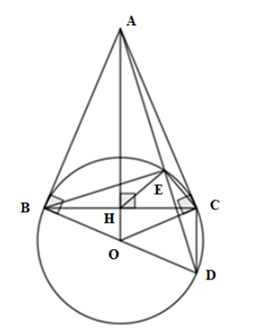
Ta có AB, AC là hai tiếp tuyến của (O) nên \(\widehat {ABO} = \widehat {AC{\rm{O}}} = 90^\circ \)
Suy ra B, C cùng thuộc đường tròn đường kính OA
Nên A, B, O, C cùng thuộc một đường tròn đường kính OA. Do đó A sai.
Ta có AB, AC là hai tiếp tuyến của (O) cắt nhau tại A
Nên AB = AC và AO là phân giác của \(\widehat {BAC}\) (tính chất 2 tiếp tuyến cắt nhau)
Suy ra ∆ ABC là tam giác cân tại A
Do đó AO vừa là phân giác của \(\widehat {BAC}\) vừa là đường trung trực của BC (tính chất tam giác cân) nên B sai
Vậy ta chọn đáp án D.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
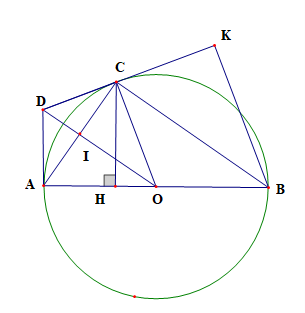
a) Xét tam giác ABC có O, I lần lượt là trung điểm của AB, AC
Suy ra OI là đường trung bình
Do đó OI // BC
b) Vì C thuộc đường tròn đường kính AB nên tam giác ABC nội tiếp (O)
Suy ra tam giác ABC vuông tại C
Xét (O) có AC là dây cung; I là trung điểm của AC
Suy ra OI là trung trực của AC
Mà D ∈ OI nên DA = DC
Xét ∆ADO và ∆CDO có
DA = DC (chứng minh trên)
DO là cạnh chung
OA = OC
Suy ra ∆ADO = ∆CDO (c.c.c)
Do đó \(\widehat {A{\rm{D}}O} = \widehat {AC{\rm{O}}}\) (hai góc tương ứng)
Mà \(\widehat {AC{\rm{O}}} = 90^\circ \) nên \(\widehat {A{\rm{D}}O} = 90^\circ \), hay AO ⊥ AD
Mà AO là bán kính của (O)
Do đó DA là tiếp tuyến của đường tròn tâm O
c) Ta có CO ⊥ CD, BK ⊥ CD
Suy ra CO // BK (quan hệ từ vuông góc đến song song)
Do đó \(\widehat {OCB} = \widehat {CBK}\) (hai góc so le trong)
Mà \(\widehat {CBO} = \widehat {OCB}\) nên \(\widehat {CBO} = \widehat {CKB}\)
Xét ∆BCH và ∆BCK có
\(\widehat {BHC} = \widehat {BKC}\left( { = 90^\circ } \right)\);
BC là cạnh chung;
\(\widehat {CBO} = \widehat {CKB}\) (chứng minh trên)
Suy ra ∆BCH = ∆BCK (cạnh huyền – góc nhọn)
Do đó CH = CK
Xét tam giác ABC vuông tại C có CH ⊥ AB, theo hệ thức lượng trong tam giác vuông ta có CH2 = HA . HB
Suy ra CK2 = HA . HB.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
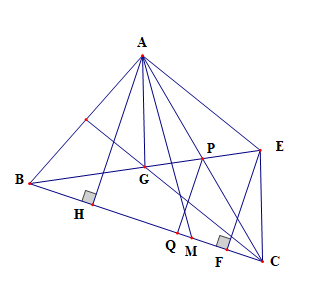
Dựng hình bình hành AGCE
Ta có \(\overrightarrow {MA} + \overrightarrow {GC} = \overrightarrow {MA} + \overrightarrow {A{\rm{E}}} = \overrightarrow {ME} \)
Kẻ EF ⊥ BC (F ∈ BC)
Khi đó \(\left| {\overrightarrow {MA} + \overrightarrow {GC} } \right| = \left| {\overrightarrow {ME} = ME} \right| \ge EF\)
Do đó \(\left| {\overrightarrow {MA} + \overrightarrow {GC} } \right|\) đạt giá trị nhỏ nhất khi M ≡ F
Gọi P là trung điểm của AC, Q là hình chiếu vuông góc của P lên BC
Vì AGCE là hình bình hành, P là trung điểm của AC
Suy ra P là trung điểm của GE
Do đó \(GP = PE = \frac{1}{2}GE\)
Vì G là trọng tâm tam giác ABC, BP là trung tuyến
Suy ra \(BG = \frac{2}{3}BP,GP = \frac{1}{3}BP\)
Ta có: BE = BP + PE
Hay \(BE = BP + \frac{1}{3}BP = \frac{4}{3}BP\)
Xét ∆BPQ và ∆BEF có
\(\widehat {FBE}\) là góc chung;
\(\widehat {BQP} = \widehat {BF{\rm{E}}}\left( { = 90^\circ } \right)\)
Suy ra (g.g)
Do đó \(\frac{{BP}}{{BE}} = \frac{{BQ}}{{BF}} = \frac{3}{4}\)
Hay \(\overrightarrow {BF} = \frac{4}{3}\overrightarrow {BQ} \)
Xét DAHC có P là trung điểm của AC và AH // PQ (vì cùng vuông góc với BC)
Suy ra Q là trung điểm của CH
Hay \(\overrightarrow {HQ} = \frac{1}{2}\overrightarrow {HC} \)
Mà \(\overrightarrow {BH} = \frac{1}{3}\overrightarrow {HC} \)
Ta có \(\overrightarrow {BQ} = \overrightarrow {BH} + \overrightarrow {HQ} = \frac{1}{3}\overrightarrow {HC} + \frac{1}{2}\overrightarrow {HC} = \frac{5}{6}\overrightarrow {HC} = \frac{5}{6}.\frac{3}{4}\overrightarrow {BC} = \frac{5}{8}\overrightarrow {BC} \)
Do đó \(\overrightarrow {BF} = \frac{4}{3}\overrightarrow {BQ} = \frac{5}{6}\overrightarrow {BC} \)
Vậy \[{\rm{x}} = \frac{5}{6}\] thì độ dài của \(\overrightarrow {MA} + \overrightarrow {GC} \) đạt giá trị nhỏ nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập