Câu hỏi:

19/08/2025 3,654

Cho nửa đường tròn đường kính AB, dây CD. Gọi H, K theo thứ tự là chân các đường vuông góc kẻ từ A, B đến CD

a) Chứng minh rằng: CH = DK

b) Chứng minh rằng: S_AHKB = S_ACB + S_ADB

c) Tính diện tích lớn nhất của tứ giác AHKB, biết AB = 30 cm, CD = 18 cm

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

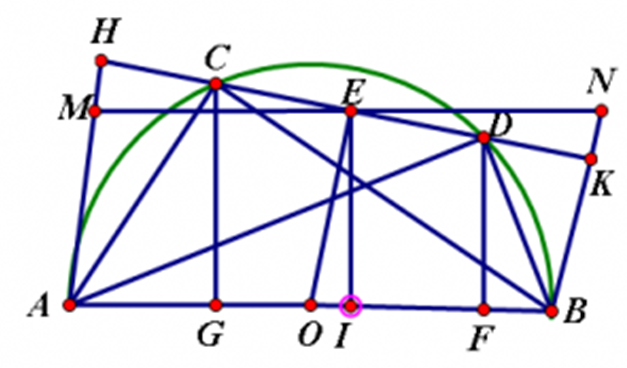
Cho nửa đường tròn đường kính AB, dây CD. Gọi H, K theo thứ tự là chân các đường (ảnh 1)

a) Gọi O là tâm đường tròn đường kính AB

Kẻ OE vuông góc với CD (E thuộc CD)

Suy ra E là trung điểm của CD

Mà OE là đường trung bình của hình thang ABKH (đi qua trung điểm một cạnh bên và song song với cạnh đáy)

Þ EH = EK mà EC = ED

Suy ra CH = DK (đpcm)

b) Hạ CG, DF ^ AB tại G, F

Þ CG // DF

Þ Tứ giác CDGF là hình thang.

Lấy I là trung điểm của GF.

Xét hình thang CDGF có:

EC = ED (E là trung điểm của CD)

IG = IF (I là trung điểm của GF)

Þ EI là đường trung bình của hình thang CDFG

\( \Rightarrow EI = \frac{{DF + CG}}{2}\)

Ta có: \[{S_{ACB}} + {S_{ADB}} = \frac{{AB + CG}}{2} + \frac{{AB + DF}}{2} = AB\,.\,\frac{{CG + DF}}{2} = AB\,.\,EI\] (1)

Qua E kẻ đường thẳng song song với AB cắt AH, BK lần lượt ở M, N.

Dễ thấy tứ giác AMNB là hình bình hành (vì có 2 cặp cạnh đối song song )

Þ S_AMNB = AB.EI

Xét ∆MHE và ∆NKE có:

\(\widehat {MEH} = \widehat {NEK}\) (2 góc đối đỉnh)

\(\widehat {MHE} = \widehat {NKE} = 90^\circ \)

EM = EN

Do đó ∆HEM = ∆KEN (cạnh huyền – góc nhọn)

Þ S_HEM = S_KEN

Khi đó:

S_AHKB = S_AMEKB + S_MHE = S_AMEKB + S_ENK = S_AMNB = AB.EI (2)

Từ (1) và (2) Þ S_AHKB = S_ACB + S_ADB

c) \({S_{AHKB}} = \frac{{\left( {AH + BK} \right)\,.\,HK}}{2} = \frac{{2OE\,.\,HK}}{2} = OE\,.\,HK\)

\(OE = \sqrt {O{D^2} - E{D^2}} = \sqrt {{{15}^2} - {9^2}} = 12\)

Þ S = 12.HK ≤ 12.AB = 12.30 = 360

Þ S_max = 360.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Rút gọn biểu thức: cos²10° + cos²20° + cos² 30° + ... + cos² 180°.

Xem đáp án

Lời giải

Ta có: cos x = − cos (180° − x) Þ cos² x = cos² (180° − x)

sin x = cos (90° − x)

sin² x + cos² x = 1

A = cos²10° + cos²20° + cos² 30° + ... + cos² 180°

= cos²10° + cos²20° + cos² 30° + ... + cos² 180°

= cos²10° + cos²20° + ... + cos² 80° + cos² 90° + cos² 80° + cos² 70° + ... + cos² 0°

= cos²0° + cos²90° + 2(cos² 10° + cos² 20° + ... + cos² 80°)

= 1 + 0 + 2(cos² 10° + cos² 20° + cos² 30° + cos² 40° + sin² 40° + sin² 30° + sin² 20° + sin² 10°)

= 1 + 0 + 2 . 4 = 9.

Câu 2

Cho hình thang ABCD vuông tại A và D. AB = AD = a, CD = 2a. Tính \(\overrightarrow {AC} \,.\,\overrightarrow {BD} \).

Xem đáp án

Lời giải

\(\overrightarrow {AC} \,.\,\overrightarrow {BD} = \left( {\overrightarrow {AD} \, + \,\overrightarrow {DC} } \right)\left( {\overrightarrow {BA} \, + \,\overrightarrow {AD} } \right)\)

\( = \overrightarrow {AD} \,.\,\overrightarrow {BA} + {\overrightarrow {AD} ^2} + \overrightarrow {DC} \,.\,\overrightarrow {BA} + \overrightarrow {DC} \,.\,\overrightarrow {AD} \)

\( = {\overrightarrow {AD} ^2} - \overrightarrow {AB} \,.\,\overrightarrow {DC} = {a^2} - a\,.\,2a = - {a^2}\)

Câu 3