Câu hỏi:
04/07/2023 931
Cho nửa đường tròn tâm O đường kính AB, M là một điểm bất kỳ thuộc nửa đường tròn (M khác A, B). Tiếp tuyến tại M cắt các tiếp tuyến Ax và By của nửa đường tròn đó lần lượt tại C và D. Gọi K là giao điểm của BM với Ax. Tìm giá trị nhỏ nhất của tổng diện tích hai tam giác ACM và BDM.
Cho nửa đường tròn tâm O đường kính AB, M là một điểm bất kỳ thuộc nửa đường tròn (M khác A, B). Tiếp tuyến tại M cắt các tiếp tuyến Ax và By của nửa đường tròn đó lần lượt tại C và D. Gọi K là giao điểm của BM với Ax. Tìm giá trị nhỏ nhất của tổng diện tích hai tam giác ACM và BDM.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
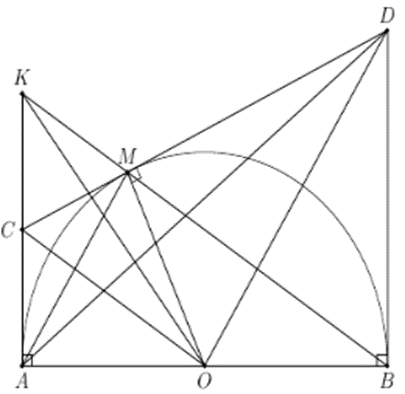
Ta có: SCAM + SMBD = SCABD − SAMB nhỏ nhất khi SCABD nhỏ nhất và SAMB lớn nhất
Ta thấy SAMB lớn nhất khi M là điểm chính giữa (dễ dàng chứng minh)
Mặt khác: \({S_{CABD}} = \frac{{\left( {CA + BD} \right)\,.\,AB}}{2} = \left( {CA + BD} \right)\,.\,R\)
\( \ge 2\sqrt {CA\,.\,BD} \,.\,R = 2\sqrt {OA\,.\,OD} \,.\,R = 2{R^2}\)
Vậy để SCABD nhỏ nhất thì CA = BD khi đó M cũng là điểm chính giữa nửa đường tròn.
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Rút gọn biểu thức: cos2 10° + cos2 20° + cos2 30° + ... + cos2 180°.
Rút gọn biểu thức: cos2 10° + cos2 20° + cos2 30° + ... + cos2 180°.
Xem đáp án »
13/07/2024
33,770
Câu 2:
Có bao nhiêu số tự nhiên có 3 chữ số khác nhau. Biết tổng của 3 chữ số này là 18.
Có bao nhiêu số tự nhiên có 3 chữ số khác nhau. Biết tổng của 3 chữ số này là 18.
Xem đáp án »
13/07/2024
22,108
Câu 3:
Cho hình thang ABCD vuông tại A và D. AB = AD = a, CD = 2a. Tính \(\overrightarrow {AC} \,.\,\overrightarrow {BD} \).
Cho hình thang ABCD vuông tại A và D. AB = AD = a, CD = 2a. Tính \(\overrightarrow {AC} \,.\,\overrightarrow {BD} \).
Xem đáp án »
13/07/2024
19,617
Câu 4:
Cho hình vuông ABCD có AC cắt BD tại O. M là điểm bất kỳ thuộc cạnh BC (M khác B, C). Tia AM cắt đường thẳng CD tại N. Trên cạnh AB lấy điểm E sao cho BE = CM.
a) Chứng minh: ∆OEM vuông cân.
b) Chứng minh: ME // BN.
c) Từ C kẻ CH vuông góc BN (H thuộc BN). Chứng minh rằng ba điểm O, M, H thẳng hàng.
Cho hình vuông ABCD có AC cắt BD tại O. M là điểm bất kỳ thuộc cạnh BC (M khác B, C). Tia AM cắt đường thẳng CD tại N. Trên cạnh AB lấy điểm E sao cho BE = CM.
a) Chứng minh: ∆OEM vuông cân.
b) Chứng minh: ME // BN.
c) Từ C kẻ CH vuông góc BN (H thuộc BN). Chứng minh rằng ba điểm O, M, H thẳng hàng.
Xem đáp án »
13/07/2024
13,209
Câu 7:
Gọi S là tập các số tự nhiên có 6 chữ số được lập từ tập hợp A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}. Chọn ngẫu nhiên một số từ tập hợp S. Tính xác suất để chọn được số tự nhiên có tích các chữ số bằng 1400.
Gọi S là tập các số tự nhiên có 6 chữ số được lập từ tập hợp A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}. Chọn ngẫu nhiên một số từ tập hợp S. Tính xác suất để chọn được số tự nhiên có tích các chữ số bằng 1400.
Xem đáp án »
13/07/2024
3,188
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận