Câu hỏi:

19/08/2025 3,890

Cho nửa đường tròn (O) đường kính AB. M là trung điểm OA. N là điểm bất kỳ thuộc nửa đường tròn. Qua N kẻ đường thẳng vuông góc với MN cắt các tiếp tuyến tại A và B tại C và D. Tìm vị trí của N để diện tích tam giác DMC min.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

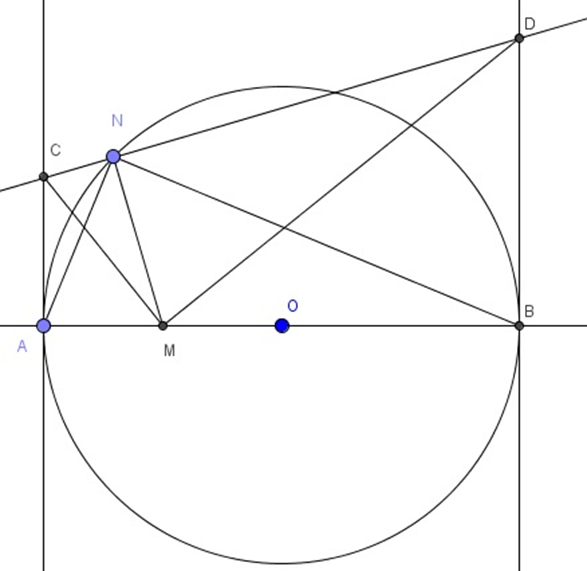
Cho nửa đường tròn (O) đường kính AB. M là trung điểm OA. N là điểm bất kỳ (ảnh 1)

Tứ giác AMNC có \(\widehat {MAC} + \widehat {MNC} = 90^\circ + 90^\circ = 180^\circ \) nên tứ giác AMNC là tứ giác nội tiếp đường tròn

Khi đó \(\widehat {CNM} = \widehat {CMA}\) (Hai góc cùng chắn cung CA)

Chứng minh tương tự ta được MBDN là tứ giác nội tiếp nên suy ra

\(\widehat {DNB} = \widehat {DMB}\) (Hai góc cùng chắn cung DB)

Suy ra \(\widehat {CNM} + \widehat {DNB} = \widehat {CMA} + \widehat {DMB}\)

\( \Rightarrow 180^\circ - \left( {\widehat {CNM} + \widehat {DNB}} \right) = 180^\circ - \left( {\widehat {CMA} + \widehat {DMB}} \right)\)

\( \Rightarrow \widehat {ANB} = \widehat {CMD} \Rightarrow \widehat {CMD} = 90^\circ \Rightarrow CM \bot DM\)

Suy ra \[\widehat {CMA} + \widehat {DMB} = 90^\circ \]

Mà \[\widehat {CMA} + \widehat {ACM} = 90^\circ \]

Do đó \(\widehat {ACM} = \widehat {BMD}\)

Xét ∆ACM và ∆BMD có:

\(\widehat {ACM} = \widehat {BMD}\) (cmt)

\(\widehat {CAM} = \widehat {MBD} = 90^\circ \)

Suy ra ∆ACM ᔕ ∆BMD (g.g)

\( \Rightarrow \frac{{AM}}{{BD}} = \frac{{AC}}{{BM}} \Rightarrow AM\,.\,BM = BD\,.\,AC\) (không đổi)

Theo Bunhiacopxki, ta có:

(AM.BM + AC.BD)² ≤ (AM² + AC²)(BM² + BD²) = MC².MD² = 4(S_DMC)²

Þ S_DMC đạt giá trị nhỏ nhất khi AC = AM, BD = BM

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Rút gọn biểu thức: cos²10° + cos²20° + cos² 30° + ... + cos² 180°.

Xem đáp án

Lời giải

Ta có: cos x = − cos (180° − x) Þ cos² x = cos² (180° − x)

sin x = cos (90° − x)

sin² x + cos² x = 1

A = cos²10° + cos²20° + cos² 30° + ... + cos² 180°

= cos²10° + cos²20° + cos² 30° + ... + cos² 180°

= cos²10° + cos²20° + ... + cos² 80° + cos² 90° + cos² 80° + cos² 70° + ... + cos² 0°

= cos²0° + cos²90° + 2(cos² 10° + cos² 20° + ... + cos² 80°)

= 1 + 0 + 2(cos² 10° + cos² 20° + cos² 30° + cos² 40° + sin² 40° + sin² 30° + sin² 20° + sin² 10°)

= 1 + 0 + 2 . 4 = 9.

Câu 2

Cho hình thang ABCD vuông tại A và D. AB = AD = a, CD = 2a. Tính \(\overrightarrow {AC} \,.\,\overrightarrow {BD} \).

Xem đáp án

Lời giải

\(\overrightarrow {AC} \,.\,\overrightarrow {BD} = \left( {\overrightarrow {AD} \, + \,\overrightarrow {DC} } \right)\left( {\overrightarrow {BA} \, + \,\overrightarrow {AD} } \right)\)

\( = \overrightarrow {AD} \,.\,\overrightarrow {BA} + {\overrightarrow {AD} ^2} + \overrightarrow {DC} \,.\,\overrightarrow {BA} + \overrightarrow {DC} \,.\,\overrightarrow {AD} \)

\( = {\overrightarrow {AD} ^2} - \overrightarrow {AB} \,.\,\overrightarrow {DC} = {a^2} - a\,.\,2a = - {a^2}\)

Câu 3