Câu hỏi:
13/07/2024 2,821
Cho hình chữ nhật ABCD. Gọi E là điểm đối xứng của B và C.
a) Chứng minh tứ giác ACED là hình bình hành.
b) Gọi M là trung điểm của BC. Tia AM cắt tia DC tại F. Chứng minh tứ giác BDEF là hình thoi.
c) Gọi I là giao điểm của AE và DC. Tia BI cắt tia DE tại . Chứng minh \(KI = \frac{1}{6}AE.\)
Cho hình chữ nhật ABCD. Gọi E là điểm đối xứng của B và C.
a) Chứng minh tứ giác ACED là hình bình hành.
b) Gọi M là trung điểm của BC. Tia AM cắt tia DC tại F. Chứng minh tứ giác BDEF là hình thoi.
c) Gọi I là giao điểm của AE và DC. Tia BI cắt tia DE tại . Chứng minh \(KI = \frac{1}{6}AE.\)
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
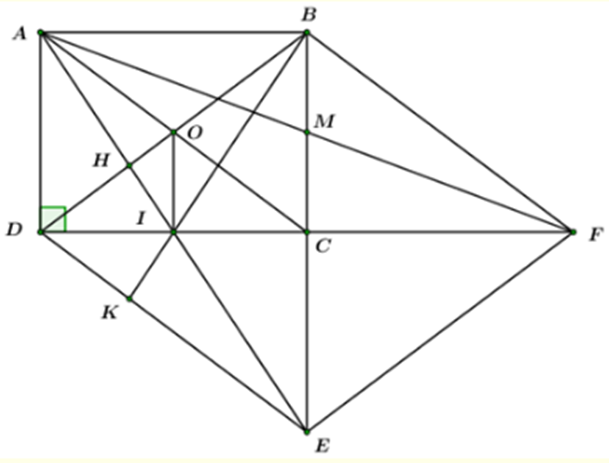
a) Ta có: E là điểm đối xứng với B qua C
Suy ra C là trung điểm của BE nên BC = EC
Xét tứ giác ACED ta có:
AD // EC (AD // BC)
AD = CE (= BC)
Suy ra ACED là hình bình hành.
b) Xét ∆ABM và ∆FCM ta có:
\[\widehat {ABM} = \widehat {FCM} = 90^\circ \]
MB = MC (gt)
\(\widehat {AMB} = \widehat {CMF}\) (Hai góc đối đỉnh)
Þ ∆ABM = ∆FCM (g.c.g)
Þ AB = CF (hai cạnh tương ứng)
Mà AB = DC (gt) Þ DC =F
Xét tứ giác BDEF ta có:
BE ^ DF
BE Ç DF = C
C là trung điểm của BE và DF
Þ BDEF là hình thoi
c) Gọi AC Ç BD = H; AI Ç BD = O
Ta có: ACED là hình bình hành
Mà AE Ç CD = I
Þ I là trung điểm của CD
Lại có O là trung điểm của AC
Þ H là trực tâm của ∆ACD
\( \Rightarrow \frac{{IH}}{{AI}} = \frac{1}{3}\)
Mà I là trung điểm của AE \( \Rightarrow AI = \frac{1}{2}AE \Rightarrow IH = \frac{1}{6}AE\)
Ta có: BDEF là hình thoi
Þ DF là tia phân giác của \(\widehat {BDE}\) (tính chất hình thoi)
\( \Rightarrow \widehat {BDC} = \widehat {CDE}\)
Ta có BDEF là hình thoi
Þ BD = DE (hai cạnh bên)
Xét ∆BDI và ∆EDI ta có:
DI chung
\(\widehat {IDB} = \widehat {IDE}\) (cmt)
BD = DE (cmt)
Þ ∆BDI = ∆EDI (c.g.c)
\( \Rightarrow \widehat {DBI} = \widehat {DEI}\) (hai góc tương ứng)
Và IE = IB (hai cạnh tương ứng)
Xét ∆HBI và ∆KEI ta có:
\(\widehat {HBI} = \widehat {KEI}\) (cmt)
IE = IB (cmt)
\(\widehat {HIB} = \widehat {KIE}\) (hai góc đối đỉnh)
Do đó ∆HBI = ∆KEI (g.c.g)
Suy ra HI = IK (hai cạnh tương ứng).
Vậy \(IK = \frac{1}{6}AE\) (đpcm)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn)
Đã bán 1,4k
₫ 280.000
₫ 150.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Rút gọn biểu thức: cos2 10° + cos2 20° + cos2 30° + ... + cos2 180°.
Rút gọn biểu thức: cos2 10° + cos2 20° + cos2 30° + ... + cos2 180°.
Xem đáp án »
13/07/2024
34,271
Câu 2:
Có bao nhiêu số tự nhiên có 3 chữ số khác nhau. Biết tổng của 3 chữ số này là 18.
Có bao nhiêu số tự nhiên có 3 chữ số khác nhau. Biết tổng của 3 chữ số này là 18.
Xem đáp án »
13/07/2024
22,587
Câu 3:
Cho hình thang ABCD vuông tại A và D. AB = AD = a, CD = 2a. Tính \(\overrightarrow {AC} \,.\,\overrightarrow {BD} \).
Cho hình thang ABCD vuông tại A và D. AB = AD = a, CD = 2a. Tính \(\overrightarrow {AC} \,.\,\overrightarrow {BD} \).
Xem đáp án »
13/07/2024
19,764
Câu 4:
Cho hình vuông ABCD có AC cắt BD tại O. M là điểm bất kỳ thuộc cạnh BC (M khác B, C). Tia AM cắt đường thẳng CD tại N. Trên cạnh AB lấy điểm E sao cho BE = CM.
a) Chứng minh: ∆OEM vuông cân.
b) Chứng minh: ME // BN.
c) Từ C kẻ CH vuông góc BN (H thuộc BN). Chứng minh rằng ba điểm O, M, H thẳng hàng.
Cho hình vuông ABCD có AC cắt BD tại O. M là điểm bất kỳ thuộc cạnh BC (M khác B, C). Tia AM cắt đường thẳng CD tại N. Trên cạnh AB lấy điểm E sao cho BE = CM.
a) Chứng minh: ∆OEM vuông cân.
b) Chứng minh: ME // BN.
c) Từ C kẻ CH vuông góc BN (H thuộc BN). Chứng minh rằng ba điểm O, M, H thẳng hàng.
Xem đáp án »
13/07/2024
13,552
Câu 7:
Gọi S là tập các số tự nhiên có 6 chữ số được lập từ tập hợp A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}. Chọn ngẫu nhiên một số từ tập hợp S. Tính xác suất để chọn được số tự nhiên có tích các chữ số bằng 1400.
Gọi S là tập các số tự nhiên có 6 chữ số được lập từ tập hợp A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}. Chọn ngẫu nhiên một số từ tập hợp S. Tính xác suất để chọn được số tự nhiên có tích các chữ số bằng 1400.
Xem đáp án »
13/07/2024
3,425
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận