Câu hỏi:
13/07/2024 16,382
Cho tứ diện đều ABCD, cạnh a. Gọi I, J lần lượt là trung điểm của AC, BC. Gọi K là một điểm trên cạnh BD sao cho KB = 2KD.
a) Xác định thiết diện của tứ diện với mặt phẳng (IJK). Chứng minh thiết diện là hình thang cân.
b) Tính diện tích thiết diện đó.
Cho tứ diện đều ABCD, cạnh a. Gọi I, J lần lượt là trung điểm của AC, BC. Gọi K là một điểm trên cạnh BD sao cho KB = 2KD.
a) Xác định thiết diện của tứ diện với mặt phẳng (IJK). Chứng minh thiết diện là hình thang cân.
b) Tính diện tích thiết diện đó.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
a) Trong (BCD): gọi M = JK ∩ CD.
Trong (ACD): gọi N = IM ∩ AD.
Ta có:
⦁ (IJK) ∩ (ABC) = IJ.
⦁ (IJK) ∩ (BCD) = JK.
⦁ (IJK) ∩ (ABD) = KN.
⦁ (IJK) ∩ (ACD) = NI.
Suy ra thiết diện của tứ diện với mặt phẳng (IJK) là tứ giác IJKN.
Ta có I, J lần lượt là trung điểm của AC, BC.
Suy ra IJ là đường trung bình của tam giác ABC.
Do đó IJ // AB.
Mà IJK) ∩ (ABD) = KN.
Vì vậy KN // AB // IJ (1)
Áp dụng định lí Thales, ta có \(\frac{{AN}}{{DA}} = \frac{{BK}}{{DB}} = \frac{2}{3}\).
Mà BD = AD (do ABCD là tứ diện đều).
Suy ra AN = BK.
Ta có ∆AIN = ∆BJK (c.g.c).
Suy ra IN = JK (2)
Từ (1), (2), suy ra tứ giác IJKN là hình thang cân.
b) Kẻ NH ⊥ IJ tại H và KE ⊥ IJ tại E.
Ta có \(IJ = \frac{{AB}}{2} = \frac{a}{2}\); \(NK = \frac{1}{3}AB = \frac{a}{3}\);\(BJ = \frac{{BC}}{2} = \frac{a}{2}\) và \(BK = \frac{2}{3}BD = \frac{{2a}}{3}\).
Ta có IH = EJ và NK = HE.
Suy ra \(IH = \frac{{IJ - NK}}{2} = \frac{{\frac{a}{2} - \frac{a}{3}}}{2} = \frac{a}{{12}}\).
Ta có \[J{K^2} = B{J^2} + B{K^2} - 2BJ.BK.\cos \widehat {JBK}\]
\[ = \frac{{{a^2}}}{4} + \frac{{4{a^2}}}{9} - 2.\frac{a}{2}.\frac{{2a}}{3}.\cos 60^\circ = \frac{{13{a^2}}}{{36}}\].
Suy ra \(NI = JK = \frac{{a\sqrt {13} }}{6}\).
Tam giác NIH vuông tại H:
\(NH = \sqrt {N{I^2} - I{H^2}} = \sqrt {\frac{{13{a^2}}}{{36}} - \frac{{{a^2}}}{{144}}} = \frac{{a\sqrt {51} }}{{12}}\).
Diện tích hình thang IJKN là:
\(S = \frac{{NH.\left( {NK + IJ} \right)}}{2} = \frac{{\frac{{a\sqrt {51} }}{{12}}.\left( {\frac{a}{3} + \frac{a}{2}} \right)}}{2} = \frac{{5{a^2}\sqrt {51} }}{{144}}\).
Vậy diện tích thiết diện bằng \(\frac{{5{a^2}\sqrt {51} }}{{144}}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Hàm số đã cho có a = 1 > 0 và \(\frac{{ - b}}{{2a}} = m + 1\) nên hàm số đã cho đồng biến trên khoảng (m + 1; +∞).
Do đó để hàm số đã cho đồng biến trên khoảng (4; 2018) thì (4; 2018) ⊂ (m + 1; +∞).
⇔ m + 1 ≤ 4 ⇔ m ≤ 3.
Mà m là số nguyên dương.
Suy ra m ∈ {1; 2; 3}.
Vậy có 3 giá trị nguyên dương của tham số m thỏa mãn yêu cầu bài toán.
Lời giải
Lời giải
Gọi x là số ha đất trồng ngô, y là số ha đất trồng đậu xanh.
Ta có các điều kiện ràng buộc đối với x, y như sau:
⦁ Hiển nhiên x ≥ 0, y ≥ 0.
⦁ Diện tích canh tác không vượt quá 8 ha nên ta có x + y ≤ 8.
⦁ Số ngày công sử dụng không vượt quá 180 ngày nên 20x + 30y ≤ 180.
⇔ 2x + 3y ≤ 18.
Từ đó, ta có hệ bất phương trình mô tả các điều kiện ràng buộc là:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 8\\2x + 3y \le 18\end{array} \right.\,\,\left( * \right)\).
Yêu cầu bài toán ⇔ Tìm (x; y) thỏa (*) để F(x; y) = 40x + 50y đạt giá trị lớn nhất.
Vẽ và xác định miền nghiệm của (*):
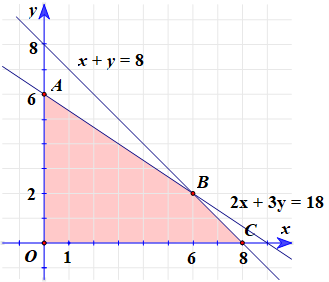
Ta có:
⦁ Miền nghiệm của (*) là tứ giác OABC (kể cả biên).
⦁ O(0; 0), A(0; 6), B(6; 2), C(8; 0).
⦁ F(O) = 0, F(A) = 300, F(B) = 340, F(C) = 320.
Suy ra maxF(x; y) = F(B) = 340 khi và chỉ khi x = 6, y = 2.
Vậy để thu được nhiều tiền nhất thì bác Năm cần trồng 6 ha ngô và 2 ha đậu xanh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận