Từ điểm M nằm ngoài đường tròn (O) kẻ các tiếp tuyến MP và MQ với đường tròn biết tam giác MPQ đều cạnh bằng \[15\sqrt 3 \]cm. Tính đường kính của đường tròn.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

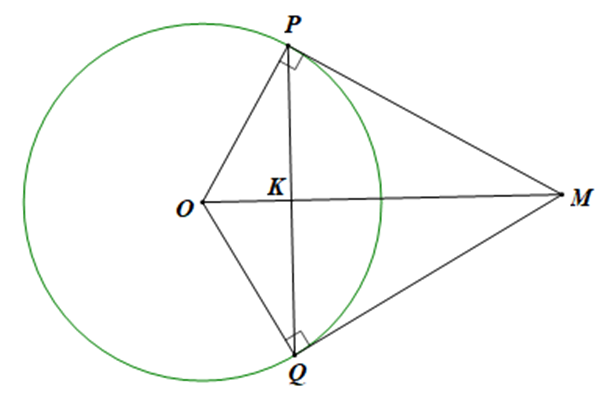
Từ điểm M nằm ngoài đường tròn (O) kẻ các tiếp tuyến MP và MQ với đường tròn (ảnh 1)

Gọi K là trung điểm của PQ \[ \Rightarrow PK = \frac{1}{2}PQ = \frac{{15\sqrt 3 }}{2}\]

Vì MP là tiếp tuyến của đườn tròn (O) ⇒ OP ⊥ PM \[ \Rightarrow \widehat {OPM} = {90^{\rm{o}}}\]

∆MPQ đều \[ \Rightarrow \widehat {MPQ} = {60^{\rm{o}}}\]\[ \Rightarrow \widehat {OPQ} = \widehat {OPM} - \widehat {MPQ} = {90^{\rm{o}}} - {60^{\rm{o}}} = {30^{\rm{o}}}\]

Xét tam giác OPK có: \[\cos \widehat {OPQ} = \frac{{PK}}{{OP}}\]

\[ \Rightarrow \cos {30^{\rm{o}}} = \frac{{\frac{{15\sqrt 3 }}{2}}}{{OP}}\] \[ \Rightarrow OP = \frac{{15\sqrt 3 }}{2}:\frac{{\sqrt 3 }}{2} = 15\]

Vậy đường kính của đường tròn là: 15.2 = 30 (cm).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình bình hành ABCD, đường chéo BD. Kẻ AH và CK vuông góc với BD ở H và ở K. Chứng minh tứ giác AHCK là hình bình hành.

Xem đáp án

Lời giải

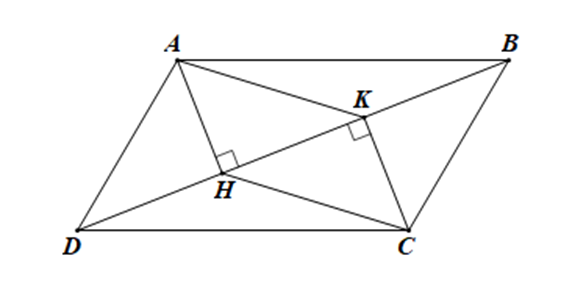
Cho hình bình hành ABCD, đường chéo BD. Kẻ AH và CK vuông góc với BD ở H (ảnh 1)

Ta có:

AH ⊥ BD, CK ⊥ BD ⇒ AH // CK (1)

∆ABH và ∆CDK có:

\(\widehat {AHB} = \widehat {CKD}\) (= 90°)

\(\widehat {ABH} = \widehat {CDK}\) (2 góc so le trong)

AB = CD (tính chất hình bình hành)

⇒ ∆ABH = ∆CDK (cạnh huyền – góc nhọn)

⇒ AH = CK (2)

Từ (1), (2) ⇒ tứ giác AHCK là hình bình hành. \[\]

Câu 2

Từ các chữ số của tập hợp {0; 1; 2; 3; 4; 5}, có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau mà trong đó nhất thiết phải có mặt chữ số 0?

Xem đáp án

Lời giải

Số cách đặt chữ số 0 là 4.

Số cách chọn số vào 4 vị trí còn lại là: \[A_5^4 = 120\].

⇒ Số số lập thành là: 4.120 = 480 (số).

Câu 3