Cho tam giác ABC có E là trung điểm của AC. Qua E kẻ ED // AB (D thuộc BC), EF // BC (F thuộc AB) cho tam giác ABC có E là trung điểm của AC. Chứng minh rằng tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.
Cho tam giác ABC có E là trung điểm của AC. Qua E kẻ ED // AB (D thuộc BC), EF // BC (F thuộc AB) cho tam giác ABC có E là trung điểm của AC. Chứng minh rằng tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
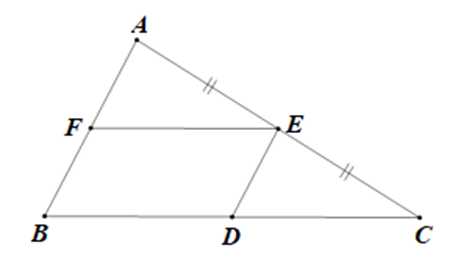
Xét ΔABC có: E là trung điểm của AC và ED // AB
Do đó: D là trung điểm của BC.
Xét ΔABC có: E là trung điểm của AC và EF // BC
Do đó: F là trung điểm của AB.
Xét ΔABC có: F, E lần lượt là trung điểm của AB, AC
Do đó: FE là đường trung bình của ΔBAC.
⇒ FE // BD và FE = BD
Suy ra FEDB là hình bình hành.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
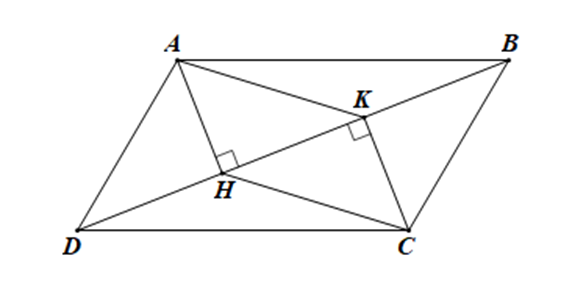
Ta có:
AH ⊥ BD, CK ⊥ BD ⇒ AH // CK (1)
∆ABH và ∆CDK có:
\(\widehat {AHB} = \widehat {CKD}\) (= 90°)
\(\widehat {ABH} = \widehat {CDK}\) (2 góc so le trong)
AB = CD (tính chất hình bình hành)
⇒ ∆ABH = ∆CDK (cạnh huyền – góc nhọn)
⇒ AH = CK (2)
Từ (1), (2) ⇒ tứ giác AHCK là hình bình hành. \[\]
Lời giải
Số cách đặt chữ số 0 là 4.
Số cách chọn số vào 4 vị trí còn lại là: \[A_5^4 = 120\].
⇒ Số số lập thành là: 4.120 = 480 (số).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.