Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày radio kiểu hai sản xuất trên dây chuyền 2 với công suất 80 radio/ngày. Để sản xuất một chiếc radio kiểu một cần 12 linh kiện, để sản xuất một chiếc radio kiểu 2 cần 9 linh kiện tiền lãi khi bán một chiếc radio kiểu một là 250 000 đồng tiền lãi thu được khi bán một chiếc Rario kiểu 2 là 180 000 đồng. Hỏi cần sản xuất như thế nào để tiền lãi thu được là nhiều nhất biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900.
Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày radio kiểu hai sản xuất trên dây chuyền 2 với công suất 80 radio/ngày. Để sản xuất một chiếc radio kiểu một cần 12 linh kiện, để sản xuất một chiếc radio kiểu 2 cần 9 linh kiện tiền lãi khi bán một chiếc radio kiểu một là 250 000 đồng tiền lãi thu được khi bán một chiếc Rario kiểu 2 là 180 000 đồng. Hỏi cần sản xuất như thế nào để tiền lãi thu được là nhiều nhất biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi số radio kiểu một và kiểu hai mà công ty này sản xuất trong một ngày lần lượt là x, y (x, y ∈ N*,chiếc)
Số tiền lãi công ty thu được trong 1 ngày:
f(x, y) = 250x + 180y (nghìn đồng)
Công suất của dây chuyền 1 là 45 radio/ngày và dây chuyền 2 là 80 radio/ngày
\( \Rightarrow \left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\end{array} \right.\)
Để sản xuất 1 chiếc radio kiểu một cần 12 linh kiện điện tử A và một chiếc radio kiểu hai cần 9 linh kiện này. Số linh kiện này được cung cấp mỗi ngày không quá 900
⇒ 12x + 9y ≤ 900
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\\12x + 9y \le 900\end{array} \right.\)
Miền của hệ BPT là phần mặt phẳng đậm nhất trong hình, kể cả biên
Khi đó f(x, y) đạt GTLN khi (x, y) là một trong số các điểm A(45; 0); B(45; 40); C(15; 80); D(0; 80).
Thay vào hàm f(x, y) ta có f(x, y) đạt GTLN bằng 18 450 000 đồng khi (x, y) = (45, 40).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Với 3 loại quà khác loại ta chia được thành 3 nhóm tương ứng như sau:
Nhóm (1) gồm 1 áo và 1 sữa
Nhóm (2) gồm 1 sữa và 1 cặp
Nhóm (3) gồm 1 cặp và 1 áo
Gọi x,y,z lần lượt là số học sinh nhận các suất quà thuộc nhóm (1); (2); (3)
Ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y + z = 10\\x + z = 7\\x + y = 9\\y + z = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = 3\\z = 1\end{array} \right.\)
Vậy số cách chia 10 suất quà này cho 10 học sinh là \(C_{10}^6.C_4^3.C_1^1\)
Để Việt và Nam có các phần thưởng giống nhau có các TH sau:
TH1: Việt và Nam nhận suất quà nhóm (1) có \(C_8^4.C_4^3.C_1^1\)
TH2: Việt và Nam nhận suất quà nhóm (2) có \(C_8^6.C_2^1.C_1^1\)
Tổng số cách để Việt và Nam có suất quà giống nhau là: \(C_8^4.C_4^3.C_1^1 + C_8^6.C_2^1.C_1^1\)
Vậy xác suất cần tìm là: \(P = \frac{{C_8^4.C_4^3.C_1^1 + C_8^6.C_2^1.C_1^1}}{{C_{10}^6.C_4^3.C_1^1}} = \frac{2}{5}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi x và y lần lượt là số máy giặt và tủ lạnh anh bán được (x ; y ∈ ℕ)
Số tiền thu được: 0,6x + 1,3y (triệu đồng)
Theo bài ra, ta có bất phương trình:
0,6x + 1,3y ≥ 10 ⇔ 0,6x + 1,3y – 10 ≥ 0
Vẽ đường thẳng (d): 0,6x + 1,3y – 10 = 0 trên mặt phẳng toạ độ Oxy
Thấy điểm O(0; 0) không thuộc BPT (1) nên miền nghiệm BPT là phần mặt phẳng không chứa O, kể cả đường thẳng (d).
Vậy để nhận được từ 10 triệu đồng trở lên tiền hoa hồng thì anh An cần bán x máy giặt và y tủ lạnh sao cho (x, y) là điểm
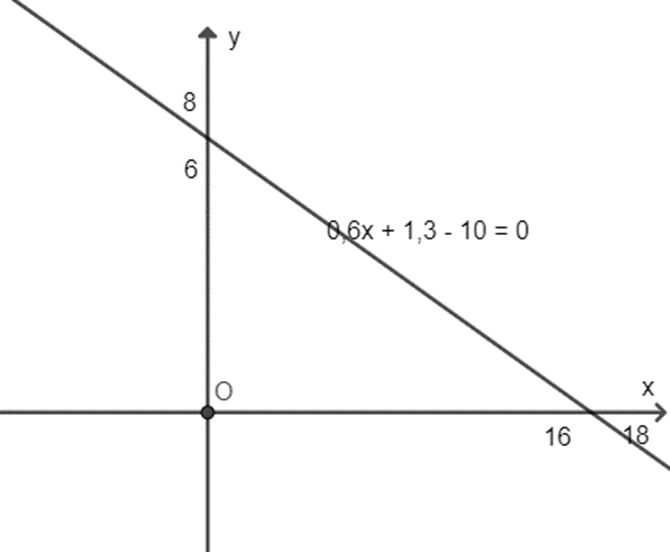
phần mặt phẳng không chứa điểm O, kể cả đường thẳng (d).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập