5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 83)
35 người thi tuần này 4.6 106.6 K lượt thi 43 câu hỏi 60 phút
- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
\[P = 5x + 3y + \frac{{12}}{x} + \frac{{16}}{y}\]
\( = 3x + \frac{{12}}{x} + y + \frac{{16}}{y} + 2\left( {x + y} \right)\)
Áp dụng Cô-si, ta có:
\(3x + \frac{{12}}{x} \ge 2\sqrt {3x.\frac{{12}}{x}} = 2.6 = 12\)
\(y + \frac{{16}}{y} \ge 2\sqrt {y.\frac{{16}}{y}} = 8\)
Lại có 2(x + y) ≥ 12
Nên P ≥ 12 + 8 + 12 = 32
Dấu “=” xảy ra khi:
\(\left\{ \begin{array}{l}3x = \frac{{12}}{x}\\y = \frac{{16}}{y}\\x + y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 4\end{array} \right.\).
Vậy Pmin = 32 khi x = 2 và y = 4.
Lời giải
a) (x + 2)(x – 4) ≥ 0
\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x + 2 \ge 0\\x - 4 \le 0\end{array} \right.\\\left\{ \begin{array}{l}x + 2 \le 0\\x - 4 \ge 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge - 2\\x \le 4\end{array} \right.\\\left\{ \begin{array}{l}x \le - 2\\x \ge 4\end{array} \right.\end{array} \right.\)
⇔ −2 ≤ x ≤ 4
Vì x ∈ ℤ nên x ∈ {−2; −1; 0; 1; 2; 3; 4}.
b) \(\frac{{2x + 3}}{{x + 4}} < 1\)
\( \Leftrightarrow \frac{{2x + 3}}{{x + 4}} - 1 < 0\)
\( \Leftrightarrow \frac{{2x + 3 - x - 4}}{{x + 4}} < 0\)
\( \Leftrightarrow \frac{{x - 1}}{{x + 4}} < 0\)
\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 1 > 0\\x + 4 < 0\end{array} \right.\\\left\{ \begin{array}{l}x - 1 < 0\\x + 4 > 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 1\\x < - 4\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\x > - 4\end{array} \right.\end{array} \right.\)
⇔ −4 < x < 1
Vì x ∈ ℤ nên x ∈ {−3; −2; −1; 0}
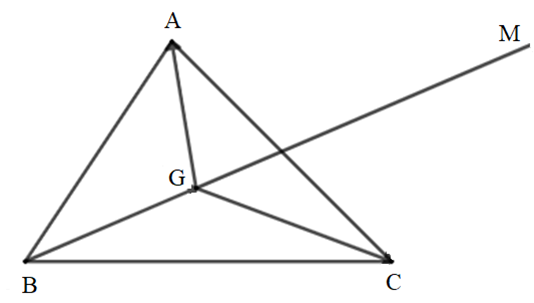
Lời giải
Gọi G là trọng tâm ∆ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
Ta có: \(VT = \overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} \)
\( = \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} - 2\overrightarrow {MB} \)
\( = \overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} - 2\overrightarrow {MB} \)
\( = 3\overrightarrow {MG} + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) - 2\overrightarrow {MB} \)
\( = 3\overrightarrow {MG} - 2\overrightarrow {MB} \)
\( = \overrightarrow {MG} + 2\overrightarrow {MG} - 2\overrightarrow {MB} \)
\( = \overrightarrow {MG} - 2\overrightarrow {GM} - 2\overrightarrow {MB} \)
\( = \overrightarrow {MG} - 2\left( {\overrightarrow {GM} + \overrightarrow {MB} } \right)\)
\( = \overrightarrow {MG} - 2\overrightarrow {GB} = VP = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {MG} = 2\overrightarrow {GB} \)
Hay \(\overrightarrow {GM} = 2\overrightarrow {GB} \)
Trên đường thẳng BG lấy điểm M sao cho GM = 2BG thì điểm M sẽ thỏa mãn đề bài.
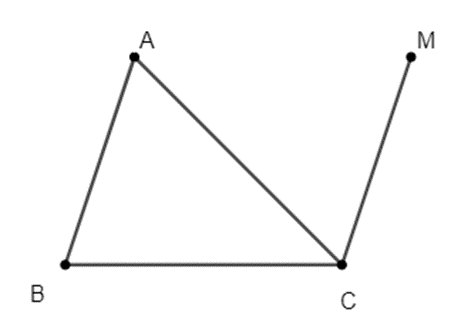
Lời giải
\(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
\( \Leftrightarrow \left( {\overrightarrow {MA} - \overrightarrow {MB} } \right) - \overrightarrow {CM} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {BA} = \overrightarrow {CM} \)
Hay M là đỉnh của hình bình hành ABCM.
Lời giải
Tốc độ trung bình của xe trong toàn bộ khoảng thời gian chuyển động là:
\({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{{v_1}{t_1} + {v_2}{t_2}}}{{{t_1} + {t_2}}} = \frac{{1.60 + 1,5.40}}{{2,5}} = 48\) (km/h)
Đáp số: 48 km/h.
Câu 6
A. 48 km/h;
B. 50 km/h;
C. 35 km/h;
D. 45 km/h.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. cos2a = cos2a – sin2a;
B. cos2a = cos2a + sin2a;
C. cos2a = 2cos2a + 1;
D. cos2a = 2sin2a – 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. R = 15 cm;
B. R = 12, 5 cm;
C. R = 7,5 cm;
D. R = 7 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.