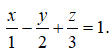66 câu trắc nghiệm: Phương trình mặt phẳng có đáp án (P1)
56 người thi tuần này 4.6 6.9 K lượt thi 31 câu hỏi 40 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. 2x - y - 3z - 8 = 0
B. x - 2z - 8 = 0
C. x - 2z - 8 = 0
D. 2x - y - 3z + 6 = 0
Lời giải
Đáp án A
Do (P) ⊥ AB nên mp(P) có một vectơ pháp tuyến là = (-2; 1; 3). Mặt khác (P) đi qua điểm A nên phương trình của mặt phẳng (P) là:
-2(x - 1) + (y - 0) + 3(z + 2) = 0 ⇔ -2x + y + 3z + 8 = 0 ⇔ 2x - y - 3z - 8 = 0.
Vậy đáp án đúng là A.
Câu 2
A. x + y + z = 0
B. x + y - z = 0
C. x - y + z = 0
D. -x + y + z = 0
Lời giải
Đáp án C
Mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với AB. Ta có
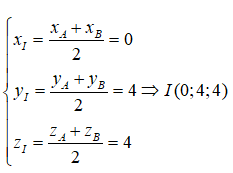
Ta chọn:
![]()
Vậy phương trình của mặt phẳng (P) là:
-2(x - 0) + 2(y - 4) - 2(z - 4) = 0 ⇔ -2x + 2y - 2z = 0 ⇔ x - y + z = 0
Vậy đáp án đúng là C.
Câu 3
A.
B. Phương trình mặt phẳng là
C. Thể tích của tứ diện bằng 4
D. Mặt phẳng () đi qua điểm A
Lời giải
Đáp án D
Vì lần lượt là hình chiếu vuông góc của điểm A(4;3;2) lên các trục Ox, Oy, Oz nên ta có (4; 0; 0), (0; 3; 0), (0; 0; 2).
Từ đó suy ra các khẳng định A và B là đúng.
Thể tích của khối tứ diện
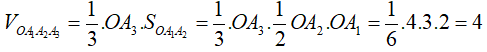
Nên khẳng định C là đúng.
Vậy khẳng định D sai.
Câu 4
A. x + y - 3 = 0
B. x - y - 1 = 0
C. 2x + y - 3z - 1 = 0
D. x - y + 1 = 0
Lời giải
Đáp án B
Mặt khác (P) đi qua điểm A(2 ;1 ;-3) nên ta có phương trình của mặt phẳng (P) là:
1(x - 2) - 1(y - 1) + 0(z + 3) = 0 x - y - 1 = 0.
Vậy đáp án đúng là B
Câu 5
A. x - y - 1 = 0
B. x - y + 1 = 0
C. x + z - 2 = 0
D. x + y - 1 = 0
Lời giải
Đáp án A
Từ giả thiết ta suy ra
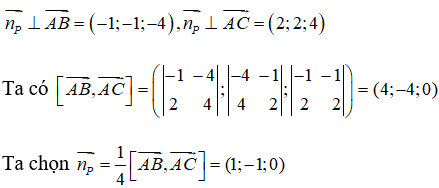
Mặt khác (P) đi qua điểm A(1 ;0 ;1) nên ta có phương trình của mặt phẳng (P) là :
1(x - 1) - 1(y - 0) + 0(z - 1) = 0 x - y - 1 = 0.
Vậy đáp án đúng là A.
Câu 6
A. 2x + 2y + z - 8 = 0
B. 2x + 2y + z + 8 = 0
C.
D. x + 2y + 2z - 9 = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. a = -4 và b = 8
B. a = -4 và b = 8 hoặc b = -4
C. a = -2 và b = 38 hoặc b = -34
D. a = -4 và b = 38 hoặc b = -34
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. (P) giao (S) theo một đường tròn
B. (P) tiếp xúc với (S)
C. (P) không cắt (S)
D. Mặt phẳng (P) đi qua tâm của mặt cầu (S)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. A + B + C = 0
B. A(x + ) + B(y + ) + C(z + ) = 0
C. A(x - ) + B(y - ) + C(z - ) = 0
D. (x - A) + (y - B) + (z - C) = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. A(x - ) - B(y - ) + C(z - ) = 0
B. A(x + ) - B(y - ) + C(z + z0) = 0
C. A(x - ) - B(y + ) + C(z - ) = 0
D. A(x + ) - B(y + ) + C(z + ) = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
B. Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
C. Khoảng cách giữa hai mặt phẳng (P) và (Q) là 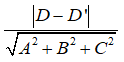
D. Khoảng cách giữa hai mặt phẳng (P) và (Q) là |D' - D|
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. Mỗi mặt phẳng chỉ có duy nhất một vectơ pháp tuyến
B. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và biết một vectơ pháp tuyến của mặt phẳng (P)
C. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và (P) vuông góc với một mặt phẳng (Q) cho trước
D. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và (P) song song với một đường thẳng d cho trước
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. Phương trình của mặt phẳng (P) đi qua điểm M(x0; y0; z0) và có một vectơ pháp tuyến = (A; B; C) là: A(x - ) + B(y - ) + C(z - ) = 0
B. Nếu hai mặt phẳng vuông góc với nhau thì hai vectơ pháp tuyến của chúng cũng vuông góc
C. Nếu hai mặt phẳng cắt nhau thì hai vectơ pháp tuyến của chúng không cùng phương
D. Nếu hai mặt phẳng (P) và (Q) có hai vectơ pháp tuyến cùng phương thì chúng song song
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. x=0
B. y=0
C. z=0
D. x+y=0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. x – 1 = 0
B. y + 2 = 0
C. z – 3 = 0
D. Đáp án khác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A.
B. x - 2y + 3z - 15 = 0
C. 3x - 6y + 2z - 18 = 0
D. 3x - 6y + 2z + 18 = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. 2x - y + 2z - 1 = 0
B. 2x - y + 2z + 9 = 0
C. 2x - y - 2z + 1 = 0
D. 2x - y + 2z + 1 = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. x + y + 1 = 0
B. -2x + y - z + 1 = 0
C. z - 1 = 0
D. z + 2 = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. 2x - y - 4z - 10 = 0
B. 2x - y - 4z + 10 = 0
C. x - y - 2z - 5 = 0
D. 2x - y - 3z + 8 = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
A. y - 2z - 2 = 0
B. y - 2z - 7 = 0
C. y - 2z + 3 = 0
D. 2y + z - 4 = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A. (1; 0; 0)
B. (0; 2; 0)
C. (0; 0; 3)
D. Phương trình của mặt phẳng (M1M2M3) là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A. 2x-3y+4z-29=0
B. 2x-3y+4z-1=0
C.
D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. 6x - 3y -2z - 6 = 0
B. x - 2y + 3z + 14 = 0
C.
D. x - 2y + 3z - 14 = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.