200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P1)
682 người thi tuần này 5.0 54.6 K lượt thi 20 câu hỏi 20 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
A. m< -2.
B. m< 1.
C. m< -3
D. m>3
Lời giải
+ Ta có: y' = x2 + 2(m+3)x + 4(m+3)
Yêu cầu của bài toán tường đương y’ =0 có hai nghiệm phân biệt x1; x2 thỏa mãn: -2 < x1< x2
Chọn C
Câu 2
A.
B. 1<m<2
C. 2< m<3
D. Đáp án khác
Lời giải
Ta có: y' =
Yêu cầu của bài toán tương đương y’ = 0 có hai nghiệm phân biệt
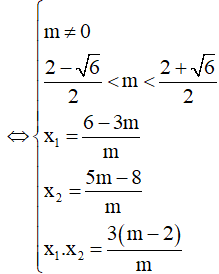
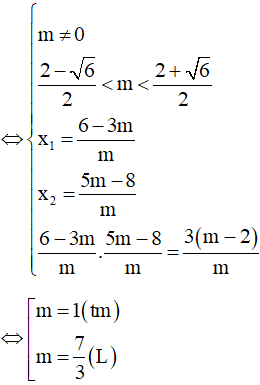
Chọn D.
Lời giải
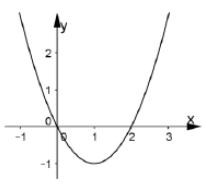
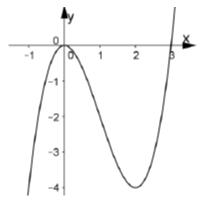
+ Ta có đạo hàm f’(x) = 3ax2+ 2bx+c .
+ Dựa vào đồ thị hàm số y = f’(x) ta thấy đồ thị hàm số đi qua các điểm (0; 0); (1; -1); (2; 0) nên a = 1/3; b = -1; c = 0.
Do vậy hàm số cần tìm có dạng y = 1/3 x3-x2+ d .
Điểm tiếp xúc với trục hoành là cực trị của đồ thị hàm số và tại đó ta có x = 0 hoặc x = 2.
+ Vì đồ thị hàm số y = f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương nên đồ thị hàm số tiếp xúc trục hoành tại điểm x = 2 nghĩa là:
f(2) = 0 hay 8/3 - 4 + d= 0 nên d = 4/3
Chọn D.
Lời giải
Chọn D.
+) Điều kiện: -4 ≤ x ≤ 4.
Ta thấy hàm số f(x) liên tục trên đoạn [ -4; 4]
đặt t =
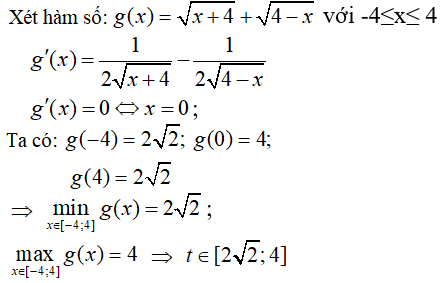
Ta có:
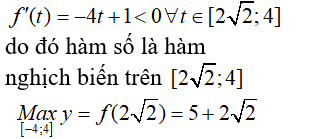
Lời giải
2x3-3x2+1 =x-1 hay 2x3-3x2-x+2=0
Khi đó ta có A(1 ; 0) ; B( x1 ; x1-1) và C( x2 ; x2-1) ( x1 ; x2 là nghiệm của (1))
Ta có , suy ra
![]()
Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 28/27
B. 4.
C. 82/27
D. 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A.m > 1
B. m > 2
C. m > -3
D. m < -2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. m= 2
B. m=3
C. m= 1
D. m= 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. m = -1
B. -1 < m < 3
C. -3 < m < -1
D. Đáp án khác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. m= -1; m= 9.
B. m= -1
C. m= 3.
D. Đáp án khác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A.
B. m> 1/ 2
C. m< 1/2
D. m
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.