200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P6)
23 người thi tuần này 5.0 54.6 K lượt thi 20 câu hỏi 20 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
+Đồ thị hàm số đã cho có TCĐ là x= 1 và TCN là y= 2; giao điểm của hai tiệm cận là
I (1; 2) .
Lấy điểm
+ Phương trình tiếp tuyến của (C ) tại M là
+ Phương trình đường thẳng MI là
+ Tiếp tuyến tại M vuông góc với MI nên ta có
Vì yêu cầu hoành độ và tung độ của M nguyên dương nên điểm cần tìm là M( 2; 3).
Chọn D.
Lời giải
+ Phương trình hoành độ giao điểm của d và (C) là
+ Theo định lí Viet ta có x1+ x2= -m ; x1.x2= ( -m-1) /2.
Gọi A( x1; y1) ; B( x2: y 2) .
+ Ta có , nên tiếp tuyến của ( C) tại A và B có hệ số góc lần lượt là
Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng - 2 khi m= -1.
Chọn B.
Câu 3
A. y= -x+1
B. y= -x
C. y= -x- 1
D. y= -x- 2
Lời giải
+ Gọi M(a; b) là toạ độ của tiếp điểm
Đạo hàm .
+ Do tam giác OAB cân tại O nên tiếp tuyến ∆ song song với đường thẳng y= -x (vì tiếp tuyến có hệ số góc âm).
Nghĩa là
-Với a= -1; b= 1 phương trình ∆: y- 1= -( x+ 1) hay y= -x ( loại) .
-Với a= -2; b= 0 thì ∆ : y- 0= -( x+ 2) hay y=-x-2 (nhận).
Vậy phương trình tiếp tuyến cần tìm là y= -x- 2.
Chọn D.
Câu 4
A. Đồ thị hàm số không có tiệm cận ngang và có đúng một tiệm cận đứng là x= -1
B. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng y= -2; y= 2 và không có tiệm cận đứng.
C. Đồ thị hàm số không có tiệm cận ngang và có đúng hai tiệm cận đứng là các đường thẳng.
D. Tất cả sai.
Lời giải
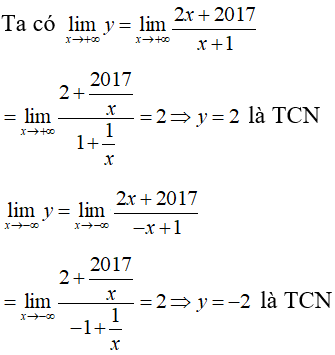
Suy ra đồ thị hàm số có 2TCN là y= 2 và y= -2 .
Chọn B.
Câu 5
A. (1; 3/2)
B. (0;1)
C. (-1; 0)
D. (3/2; 2)
Lời giải
PT hoành độ giao điểm là
(3m-1) x+ 6m+ 3 = x3-3x2+ 1 hay x3-3x2 – (3m-1) x-6m-2=0 ( *)
Giả sử A( x1; y1) ; B( x2; y2); B( x3; y3) lần lượt là giao điểm của (C) và (d)
Vì B cách đều hai điểm A và C nên B là trung điểm của AC
Suy ra x1+ x3= 2x2
Thay x2 = 1vào , ta có
Vậy -1< m< 0
Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. m=0 hoặc m= 6
B. m> 0 hoặc m< 6
C. 0< m< 3
D. 1< m< 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. - 2
B. -3
C. - 4
D. -5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A.
B.
C.
D. Không tồn tại giá trị nhỏ nhất của g( x) trên [-3;3]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. 5
B. 4
C. 3
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. Hai điểm M và N đối xứng nhau qua gốc tọa độ.
B. Đường tiệm cận ngang của đồ thị hàm số đi qua trung điểm của đoạn thẳng MN.
C. Hai điểm M và N đối xứng nhau qua giao điểm của hai đường tiệm cận.
D. Đường tiệm cận đứng của đồ thị hàm số đi qua trung điểm của đoạn thẳng MN.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.