Cho hàm số có đồ thị (C) và điểm I (1; 2). Điểm M( a; b) ; a> 0 thuộc (C) sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM.
Giá trị a+ b bằng
A. 3
B . 4
C. 5
D. 6
Quảng cáo
Trả lời:
Hệ số góc của đường thẳng IM là:
Mặt khác tiếp tuyến tại M có hệ số góc
Giả thiết bài toán
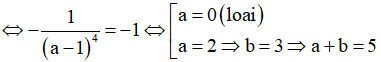
Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.
B.
C.
D. Không tồn tại giá trị nhỏ nhất của g( x) trên [-3;3]
Lời giải
Ta có:
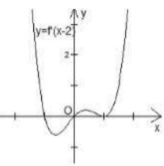
+ Với x< - 3 ta có: f’ (x)< x + 1 suy ra hàm số nghịch biến trên khoảng ( -∞; -3)
+ Xét hàm số g( x) ; ta cần so sánh g(-3) và g( 3)
Ta có g(x) = 2f(x) – ( x + 1) 2 nên g’(x) = 2f’(x) - 2(x + 1)
Phương trình (Dựa vào đồ thị hàm số y= f’ (x)) .
Bảng xét dấu của g’(x)
Dựa vào bảng xét dấu, ta được
Dựa vào hình vẽ lại có
Do đó g( 1) – g( -3) > g( 1) – g( 3) hay g( 3) > g( -3) .
Suy ra GTNN của hàm số trên đoạn [- 3; 3] là g( -3) .
Chọn B.
Lời giải
Theo bài ra, thanh sào sẽ đi qua các điểm B, M , C (hình vẽ dưới)
Suy ra độ dài thanh sào là
Đặt ,do đó
Yêu cầu bài toán
Ta có
Suy ra . Vậy độ dài tối thiểu của thanh sào là
Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. - 2
B. -3
C. - 4
D. -5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Ngoc Lo
Cho hàm số y=f(x)=3x + 5
A) tính f(2)
B) hàm số trên đồng biến hay nghịch biến ? Vì sao ?
Ad giúp em với ạ. Em cảm ơn
Xem tất cả 3 phản hồi
Linh Ryes
Hàm đồng biến
Gacon
Hàm số đồng biến vì y'=3>0
trogiangvietjack
Đồng biến