Biết đường thẳng y= (3m-1) x+ 6m+3 cắt đồ thị hàm số y= x3-3x2+ 1 tại ba điểm phân biệt sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?
A. (1; 3/2)
B. (0;1)
C. (-1; 0)
D. (3/2; 2)
Quảng cáo
Trả lời:
PT hoành độ giao điểm là
(3m-1) x+ 6m+ 3 = x3-3x2+ 1 hay x3-3x2 – (3m-1) x-6m-2=0 ( *)
Giả sử A( x1; y1) ; B( x2; y2); B( x3; y3) lần lượt là giao điểm của (C) và (d)
Vì B cách đều hai điểm A và C nên B là trung điểm của AC
Suy ra x1+ x3= 2x2
Thay x2 = 1vào , ta có
Vậy -1< m< 0
Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.
B.
C.
D. Không tồn tại giá trị nhỏ nhất của g( x) trên [-3;3]
Lời giải
Ta có:
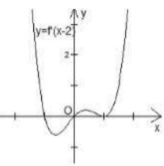
+ Với x< - 3 ta có: f’ (x)< x + 1 suy ra hàm số nghịch biến trên khoảng ( -∞; -3)
+ Xét hàm số g( x) ; ta cần so sánh g(-3) và g( 3)
Ta có g(x) = 2f(x) – ( x + 1) 2 nên g’(x) = 2f’(x) - 2(x + 1)
Phương trình (Dựa vào đồ thị hàm số y= f’ (x)) .
Bảng xét dấu của g’(x)
Dựa vào bảng xét dấu, ta được
Dựa vào hình vẽ lại có
Do đó g( 1) – g( -3) > g( 1) – g( 3) hay g( 3) > g( -3) .
Suy ra GTNN của hàm số trên đoạn [- 3; 3] là g( -3) .
Chọn B.
Lời giải
Theo bài ra, thanh sào sẽ đi qua các điểm B, M , C (hình vẽ dưới)
Suy ra độ dài thanh sào là
Đặt ,do đó
Yêu cầu bài toán
Ta có
Suy ra . Vậy độ dài tối thiểu của thanh sào là
Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. - 2
B. -3
C. - 4
D. -5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.