Số nguyên nhỏ nhất của tham số để PT x2+m+2x+4=m-1x3+4x có nghiệm là A. 6 B. 8 C. 7 D. 9

Điều kiện x≥ 0. Dễ thấy x = 0 không là nghiệm của phương trình. Xét x> 0 , chia cả 2 vế của phương trình cho x ta được x2+4x-(m-1)x2+4x+m+2=0 (*) Đặt t=x2+4x , khi đó phương trình ( *) trở thành: t2- (m - 1)t + m + 2 = 0 Vì t ≥ 2 nên t - 1 ≠ 0 nên phương trình (*)⇔t2+t+2=m(t-1)⇔m=t2+t+2t-1 Xét hàm số f(t)=t2+t+2t-1 trên [2; +∞)f'(t)=t2-2t-3(t-1)2⇒min[2; +∞)f(t)=7 Khi đó, để phương trình m =f( t) có nghiệm ⇔m≥min[2; +∞)f(t)=7 Chọn C.

Câu hỏi:

01/02/2021 6,677

Số nguyên nhỏ nhất của tham số để PT $x^{2} + (m + 2) x + 4 = (m - 1) \sqrt{x^{3} + 4 x}$ có nghiệm là

A. 6

B. 8

C. 7

D. 9

Xem lời giải

Câu hỏi trong đề: 200 Trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Điều kiện x≥ 0.

Dễ thấy x = 0 không là nghiệm của phương trình.

Xét x> 0 , chia cả 2 vế của phương trình cho x ta được

$\frac{x^{2} + 4}{x} - (m - 1) \sqrt{\frac{x^{2} + 4}{x}} + m + 2 = 0 (*)$

Đặt $t = \sqrt{\frac{x^{2} + 4}{x}}$ , khi đó phương trình ( *) trở thành: t²- (m - 1)t + m + 2 = 0

Vì t ≥ 2 nên t - 1 ≠ 0 nên phương trình $(*) \Leftrightarrow t^{2} + t + 2 = m (t - 1) \Leftrightarrow m = \frac{t^{2} + t + 2}{t - 1}$

Xét hàm số $f (t) = \frac{t^{2} + t + 2}{t - 1} t r ê n [2; + \infty) f' (t) = \frac{t^{2} - 2 t - 3}{{(t - 1)}^{2}} \Rightarrow \underset{[2; + \infty)}{m i n} f (t) = 7$

Khi đó, để phương trình m =f( t) có nghiệm $\Leftrightarrow m \geq \underset{[2; + \infty)}{m i n} f (t) = 7$

Chọn C.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số y= f( x) liên tục trên R Đồ thị của hàm số y= f’ (x) như hình bên. Đặt g(x) = 2f(x)-(x+ 1) ² . Mệnh đề nào dưới đây đúng?

A. $\underset{[- 3; 3]}{m i n} g (x) = g (1) .$

B. $\underset{[- 3; 3]}{m a x} g (x) = g (1) .$

C. $\underset{[- 3; 3]}{m i n} g (x) = g (3) .$

D. Không tồn tại giá trị nhỏ nhất của g( x) trên [-3;3]

Lời giải

Ta có:

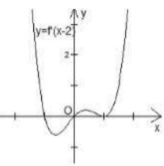
+ Với x< - 3 ta có: f’ (x)< x + 1 suy ra hàm số nghịch biến trên khoảng ( -∞; -3)

+ Xét hàm số g( x) ; ta cần so sánh g(-3) và g( 3)

Ta có g(x) = 2f(x) – ( x + 1) ² nên g’(x) = 2f’(x) - 2(x + 1)

Phương trình (Dựa vào đồ thị hàm số y= f’ (x)) .

Bảng xét dấu của g’(x)

Dựa vào bảng xét dấu, ta được $\underset{[- 3; 3]}{m a x} g (x) = g (1) .$

Dựa vào hình vẽ lại có

Do đó g( 1) – g( -3) > g( 1) – g( 3) hay g( 3) > g( -3) .

Suy ra GTNN của hàm số trên đoạn [- 3; 3] là g( -3) .

Chọn B.

Câu 2

Tìm tất cả các giá trị thực của m để đường thẳng y= x+ m-1 cắt đồ thị hàm số $y = \frac{2 x + 1}{x + 1}$ tại hai điểm phân biệt A, B sao cho $A B = 2 \sqrt{3}$

A. $m = 2 \pm \sqrt{10}$

B. $m = 4 \pm \sqrt{3}$

C. $m = 2 \pm \sqrt{3}$

D. $m = 4 \pm \sqrt{10}$

Lời giải

Phương trình hoành độ giao điểm của ( C) và d là

Để (C) cắt (d) tại hai điểm phân biệt khi và chỉ khi f( x) = 0 có hai nghiệm phân biệt

Gọi A(x₁; y₁) ; B(x₂; y₂) là giao điểm của (C) và d

Theo hệ thức Viet, ta được

mà

Chọn D.

Câu 3

Cho hàm số $y = \frac{- x + 1}{2 x - 1}$ có đồ thị là (C) , đường thẳng d: y= x+ m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B . Gọi k₁; k₂ lần lượt là hệ số góc của các tiếp tuyến với ( C) tại A; B . Tìm m để tổng k₁+ k₂ đạt giá trị lớn nhất.

A. -2

B. -1

C. 1

D. 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hàm số y= f( x) có đạo hàm $f' (x) = {(x + 1)}^{4} {(x - 2)}^{5} {(x + 3)}^{3}$ Số điểm cực trị của hàm số $f (|x|)$ là

A. 5

B. 3

C. 1

D. 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Để chặn đường hành lang hình chữ L người ta dung một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ bên). Biết rằng a = 24 và b = 3, hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu?

A. 18 $\sqrt{5}$

B. 27 $\sqrt{5}$

C. 15 $\sqrt{5}$

D. 12 $\sqrt{5}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số $y = \frac{x - a}{b x + c}$ có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A= a+ b+ c

A. - 2

B. -3

C. - 4

D. -5

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

gCho hàm số y= f( x) có đạo hàm liên tục trên R, hàm số y= f’ (x-2) có đồ thị hàm số như hình bên. Số điểm cực trị của hàm số y= f( x) là :

A. 0

B. 2

C. 1

D. 3

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Số nguyên nhỏ nhất của tham số để PT x2+m+2x+4=m-1x3+4x có nghiệm là

Bình luận

Cho hàm số y= f( x) liên tục trên R Đồ thị của hàm số y= f’ (x) như hình bên. Đặt g(x) = 2f(x)-(x+ 1) 2 . Mệnh đề nào dưới đây đúng?

Tìm tất cả các giá trị thực của m để đường thẳng y= x+ m-1 cắt đồ thị hàm số y=2x+1x+1 tại hai điểm phân biệt A, B sao cho AB=23

Cho hàm số y= f( x) có đạo hàm f'(x)=(x+1)4(x-2)5(x+3)3 Số điểm cực trị của hàm số fx là

Để chặn đường hành lang hình chữ L người ta dung một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ bên). Biết rằng a = 24 và b = 3, hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu?

Cho hàm số y=x-abx+c có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A= a+ b+ c

gCho hàm số y= f( x) có đạo hàm liên tục trên R, hàm số y= f’ (x-2) có đồ thị hàm số như hình bên. Số điểm cực trị của hàm số y= f( x) là :

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Số nguyên nhỏ nhất của tham số để PT $x^{2} + (m + 2) x + 4 = (m - 1) \sqrt{x^{3} + 4 x}$ có nghiệm là

Cho hàm số y= f( x) liên tục trên R Đồ thị của hàm số y= f’ (x) như hình bên. Đặt g(x) = 2f(x)-(x+ 1) ² . Mệnh đề nào dưới đây đúng?

Tìm tất cả các giá trị thực của m để đường thẳng y= x+ m-1 cắt đồ thị hàm số $y = \frac{2 x + 1}{x + 1}$ tại hai điểm phân biệt A, B sao cho $A B = 2 \sqrt{3}$

Cho hàm số y= f( x) có đạo hàm $f' (x) = {(x + 1)}^{4} {(x - 2)}^{5} {(x + 3)}^{3}$ Số điểm cực trị của hàm số $f (|x|)$ là

Cho hàm số $y = \frac{x - a}{b x + c}$ có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A= a+ b+ c