23 câu Chuyên đề Toán 12 Bài 3: Ứng dụng của tích phân có đáp án

50 người thi tuần này 4.6 2.9 K lượt thi 23 câu hỏi 90 phút

Câu 1

Gọi diện tích hình phẳng giới hạn bởi đồ thị hàm số \(\left( C \right)\): \(y = \frac{{ - 3x - 1}}{{x - 1}}\) và hai trục tọa độ là S. Tính S.

Xem đáp án

Lời giải

Hướng dẫn giải

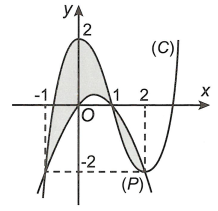
Hoành độ giao điểm của \(\left( C \right)\) và trục hoành là nghiệm của phương trình:

\(\frac{{ - 3x - 1}}{{x - 1}} = 0 \Leftrightarrow x = - \frac{1}{3}\)

Do đó diện tích hình phẳng là

\(S = \left| {\int\limits_{ - \frac{1}{3}}^0 {\frac{{ - 3x - 1}}{{x - 1}}dx} } \right| = \left| {\int\limits_{ - \frac{1}{3}}^0 {\left( {3 + \frac{4}{{x - 1}}} \right)dx} } \right|\)

\( = \left( {3x + 4\ln \left| {x - 1} \right|} \right)\left| \begin{array}{l}^0\\_{ - \frac{1}{3}}\end{array} \right. = 4\ln \frac{4}{3} - 1\)

Câu 2

Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\left( {x - 2} \right)^2} - 1\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\) bằng

A. \(\frac{2}{3}\)

B. \(\frac{3}{2}\)

C. \(\frac{1}{3}\)

D. \(\frac{7}{3}\)

Lời giải

Hướng dẫn giải

Ta có \(S = \int\limits_1^2 {\left| {{{\left( {x - 2} \right)}^2} - 1} \right|dx = } \int\limits_1^2 {\left| {{x^2} - 4x + 3} \right|dx} \)

Vì phương trình \({x^2} - 4x + 3\) không có nghiệm trên \(\left( {1;2} \right)\) nên \(S = \left| {\int\limits_1^2 {\left( {{x^2} - 4x + 3} \right)dx} } \right| = \frac{2}{3}\)

Chọn A.

Câu 3

Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = - 3\), \(x = 2\) (như hình vẽ bên). Đặt \(a = \int\limits_{ - 3}^1 {f\left( x \right)dx} \), \(b = \int\limits_1^2 {f\left( x \right)dx} \).

Mệnh đề nào sau đây là đúng?

A. \(S = a + b\).

B. \(S = a - b\).

C. \(S = - a - b\).

D. \(S = b - a\).

Lời giải

Hướng dẫn giải

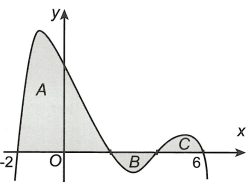
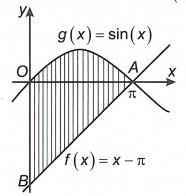
Ta có \(S = \int\limits_{ - 3}^1 {\left| {f\left( x \right)} \right|dx} + \int\limits_1^2 {\left| {f\left( x \right)} \right|dx} = - \int\limits_{ - 3}^1 {f\left( x \right)dx} + \int\limits_1^2 {f\left( x \right)dx} = - a + b\)

Chọn D.

Câu 4

Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \(y = \ln x\), \(y = 1\) và đường thẳng \(x = 1\) bằng

A. \({e^2}\).

B. \(e + 2\).

C. 2e.

D. \(e - 2\).

Lời giải

Hướng dẫn giải

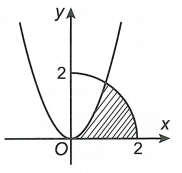
Ta có \(\ln x = 1 \Leftrightarrow x = e\).

Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \(y = \ln x\), \(y = 1\) và đường thẳng \(x = 1\) là:

\(S = \int\limits_1^e {\left| {\ln x - 1} \right|dx} = \left| {\int\limits_1^e {\left( {\ln x - 1} \right)dx} } \right| = \left| {x\left( {\ln x - 1} \right)\left| \begin{array}{l}^e\\_1\end{array} \right. - \int\limits_1^e {dx} } \right| = \left| {1 - x\left| \begin{array}{l}^e\\_1\end{array} \right.} \right| = e - 2\)

Chọn D

Câu 5

Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục hoành và các đường thẳng \(x = - 1\), \(x = 1\). Với \(k \in \left( { - 1;1} \right)\), đường thẳng \(x = k\) chia hình phẳng \(\left( H \right)\) thành hai hình phẳng có diện tích lần lượt là \({S_1}\) và \({S_2}\) (như hình vẽ bên). Giá trị k để \({S_1} = {S_2}\) là

A. \(2\ln 2 - 1\).

B. \(2\ln \left( {e - \frac{1}{e}} \right) - 1\).

C. \(\ln \left( {e + \frac{1}{e}} \right) - \ln 2\).

D. \(\ln 2\).

Lời giải

Hướng dẫn giải

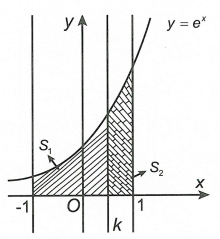
Vì \({e^x} > 0\) với mọi \(x \in \mathbb{R}\) nên ta có

\({S_1} = \int\limits_{ - 1}^k {{e^x}dx} = {e^x}\left| \begin{array}{l}^k\\_{ - 1}\end{array} \right. = {e^k} - {e^{ - 1}}\) và \({S_2} = \int\limits_k^1 {{e^x}dx} = {e^x}\left| \begin{array}{l}^1\\_k\end{array} \right. = e - {e^k}\)

\({S_1} = {S_2} \Leftrightarrow {e^k} - {e^{ - 1}} = e - {e^k} \Leftrightarrow 2{e^k} = e + \frac{1}{e} \Leftrightarrow {e^k} = \frac{1}{2}\left( {e + \frac{1}{e}} \right)\)

\( \Leftrightarrow k = \ln \frac{1}{2}\left( {e + \frac{1}{e}} \right) = \ln \left( {e + \frac{1}{e}} \right) - \ln 2\)

Chọn C.

Chú ý: \({a^x} = b \Leftrightarrow x = {\log _a}b\)

Câu 6

Cho hàm số \(y = f\left( x \right)\) có đồ thị trên \(\left[ { - 2;6} \right]\) như hình vẽ bên. Biết các miền A, B, \(x = 2\) có diện tích lần lượt là 32; 2; 3.

Tích phân \(\int\limits_{ - 2}^2 {\left[ {f\left( {2x + 2} \right) + 1} \right]dx} \) bằng

A. \(\frac{{45}}{2}\).

B. 41.

C. 37.

D. \(\frac{{41}}{2}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Bright

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý