Câu hỏi:
04/01/2023 23,660
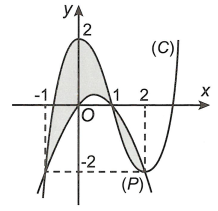
Hình phẳng \(\left( H \right)\) được giới hạn bởi đồ thị \(\left( C \right)\) của hàm đa thức bậc ba và parabol \(\left( P \right)\) có trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Vì đồ thị hàm bậc ba và đồ thị hàm bậc hai cắt trục tung tại các điểm có tung độ lần lượt là \(y = 2\) và \(y = 0\) nên ta xét hai hàm số là \(y = a{x^3} + b{x^2} + cx + 2\), \(y = m{x^2} + nx\) (với a, \(m \ne 0\)).
Suy ra \(\left( C \right)\): \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + 2\) và \(\left( P \right)\): \(y = g\left( x \right) = m{x^2} + nx\).
Phương trình hoành độ giao điểm của \(\left( C \right)\) và \(\left( P \right)\) là:
\(a{x^3} + b{x^2} + cx + 2 = m{x^2} + nx \Leftrightarrow \left( {a{x^3} + b{x^2} + cx + 2} \right) - \left( {m{x^2} + nx} \right) = 0\).
Đặt \(P\left( x \right) = \left( {a{x^3} + b{x^2} + cx + 2} \right) - \left( {m{x^2} + nx} \right)\).
Theo giả thiết, \(\left( C \right)\) và \(\left( P \right)\) cắt nhau tại các điểm có hoành độ lần lượt là \(x = - 1\), \(x = 1\), \(x = 2\) nên \(P\left( x \right) = a\left( {x + 1} \right)\left( {x - 1} \right)\left( {x - 2} \right)\).
Ta có \(P\left( 0 \right) = 2a\).
Mặt khác, ta có \(P\left( 0 \right) = f\left( 0 \right) - g\left( 0 \right) = 2 \Rightarrow a = 1\).
Vậy diện tích phần tô đậm là \(S = \int\limits_{ - 1}^2 {\left| {\left( {x + 1} \right)\left( {x - 1} \right)\left( {x - 2} \right)} \right|dx} = \frac{{37}}{{12}}\)
Chọn A.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Ta có \(S = \int\limits_1^2 {\left| {{{\left( {x - 2} \right)}^2} - 1} \right|dx = } \int\limits_1^2 {\left| {{x^2} - 4x + 3} \right|dx} \)
Vì phương trình \({x^2} - 4x + 3\) không có nghiệm trên \(\left( {1;2} \right)\) nên \(S = \left| {\int\limits_1^2 {\left( {{x^2} - 4x + 3} \right)dx} } \right| = \frac{2}{3}\)
Chọn A.
Lời giải
Hướng dẫn giải
Phương trình hoành độ giao điểm của hai đồ thị là
\({x^3} - 3x = x \Leftrightarrow {x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = \pm 2\\x = 0\end{array} \right.\)
Vậy \(S = \left| {\int\limits_{ - 2}^0 {\left( {{x^3} - 4x} \right)dx} } \right| + \left| {\int\limits_0^2 {\left( {{x^3} - 4x} \right)dx} } \right| = 4 + 4 = 8\).
Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận