5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 26)
31 người thi tuần này 4.6 106.6 K lượt thi 63 câu hỏi 50 phút
- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Biến đổi vế trái:
(a + b + c)3 = [(a + b) + c]3
= (a + b)3 + 3(a + b)2c + 3(a +b)c2 + c3
= a3 + 3a2b + 3ab2 + b3 + 3(a2 + 2ab + b2)c + 3ac2 + 3bc2 + c3
= a3 + 3a2b + 3ab2 + b3 + 3a2c + 6abc + 3b2c + 3ac2 + 3bc2 + c3
= a3 + b3 + c3 + 3a2b + 3ab2 + 3a2c + 6abc + 3b2c + 3ac2 + 3bc2
= a3 + b3 + c3 + (3a2b + 3ab2) + (3a2c + 3abc) + (3abc + 3bc2) + (3ac2 + 3bc2)
= a3 + b3 + c3 + 3ab(a + b) + 3ac(a + b) + 3bc(a + c) + 3c2(a + b)
= a3 + b3 + c3 + (a + b)(3ab + 3ac + 3bc + 3c2)
= a3 + b3 + c3 + (a + b)[(3ab + 3ac) + (3bc + 3c2)]
= a3 + b3 + c3 + (a + b)[3a(b + c) + 3c(b + c)]
= a3 + b3 + c3 + 3(a + b)(b + c)(a + c) (đpcm)
Lời giải
Ta có: A = a3 + b3 + c3 – 3abc
= (a3 + b3) + c3 – 3abc
= (a + b)3 – 3ab(a + b) + c3 – 3abc
= [(a + b)3 + c3] – [3ab(a + b) – 3abc]
= (a + b + c)[(a + b)2 – (a + b)c + c2] – 3ab(a + b + c)
= (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
Mà a + b + c = 0 nên suy ra:
A = 0 \[ \Rightarrow \]a3 + b3 + c3 – 3abc = 0
\( \Leftrightarrow \) a3 + b3 + c3 = 3abc (đpcm).
Câu 3
A. (1; 3);
B. x > 3;
C. x < −2;
D. Đáp án khác.
Lời giải
Đáp án đúng là: D
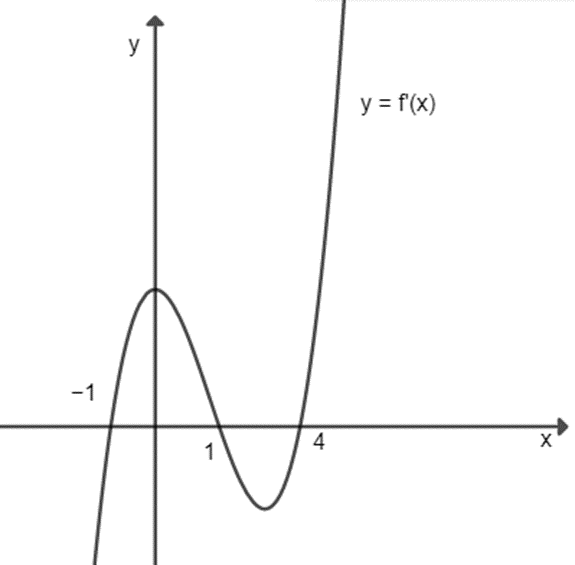
Ta có \({\left( {f\left( {2 - x} \right)} \right)^\prime } = {\left( {2 - x} \right)^\prime }.f'\left( {2 - x} \right) = - f'\left( {2 - x} \right)\).
Hàm số đồng biến khi \(\left( {f\left( {2 - x} \right)} \right)' > 0\)
\( \Leftrightarrow f'(2 - x) \Leftrightarrow \left[ \begin{array}{l}2 - x < - 1\\1 < 2 - x < 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 3\\ - 2 < x < 1\end{array} \right.\).
Câu 4
A. \(\frac{2}{5}\);
B. \(\frac{1}{{10}}\);
C. \(\frac{1}{5}\);
D. \(\frac{1}{4}\).
Lời giải
Đáp án đúng là: C
Xét ngẫu nhiên 10 học sinh thành một hàng có 10! cách ⇒ n(Ω) = 10!
Gọi biến cố “Xếp 10 học sinh thành một hàng sao cho An và Bình đứng cạnh nhau”.
Xem An và Bình là nhóm X.
Xếp X và 8 học sinh còn lại có 9! (cách).
Hoán vị An và Bình trong X có 2! (cách).
Vậy có 9!2! cách ⇒ n(A) = 9!2!
Xác suất của biến cố A là: \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{9!2!}}{{10!}} = \frac{{9!2}}{{10.9!}} = \frac{1}{5}\).
Lời giải
Đáp án đúng là: C
Xếp 10 học sinh sao có nam nữ ngồi xen kẽ.
Xếp 5 học sinh nam có 5! cách, xếp 5 học sinh nữ vào 5 vị trí còn lại có 5! cách.
Đổi chỗ nam và nữ có 2 cách.
Suy ra có 2.(5!)2 cách xếp 10 học sinh sao có nam nữ ngồi xen kẽ.
* Xếp 8 học sinh không có An và Bình trước:
• TH1:
+ Học sinh nam đứng đầu hàng, có (4!)2 cách.
+ Xếp An và Bình vào 1 trong 9 vị trí gồm 7 vị trí giữa 2 học sinh liền kề nhau và 2 vị trí biên. Ứng với mỗi vị trí có 1 cách xếp An và Bình sao cho thỏa mãn yêu cầu, do đó có 9 cách xếp.
Vậy có 9.(4!)2 cách.
• TH2:
+ Học sinh nữ đứng đầu hàng, tương tự TH1 có 9.(4!)2 (cách).
Suy ra số cách xếp 10 học sinh xen kẽ mà An luôn cạnh Bình là 2.9.(4!)2 (cách).
Vậy số cách sắp xếp nam và nữ ngồi xen kẽ, đồng thời An không ngồi cạnh Bình là:
2.(5!)2 – 2.9.(4!)2 = 2.5.5.(4!)2 – 18.(4!)2 = 32.(4!)2 (cách)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 2;
B. 1;
C. 4;
D. 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \(\frac{{3{a^3}}}{4}\);
B. \(\frac{{{a^2}}}{4}\);
C. \(\frac{{2{a^3}}}{3}\);
D. \(\frac{{3{a^3}}}{8}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
A. 4033;
B. 2017;
C. 4034;
D. 4035.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
A. [1; 2];
B. [0; 2];
C. [1; 3];
D. [2; 3].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. \(\left[ { - \frac{3}{4};\frac{{61}}{4}} \right]\);
B. \(\left[ {\frac{{11}}{4};\frac{{61}}{4}} \right]\);
C. \(\left[ { - \frac{{11}}{4};\frac{{61}}{4}} \right]\);
D. \(\left[ {\frac{3}{4};\frac{{61}}{4}} \right]\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 47
A. \(\overrightarrow {AF} + \overrightarrow {CE} + \overrightarrow {DB} \);
B. \(\overrightarrow {AE} + \overrightarrow {CB} + \overrightarrow {DF} \);
C. \(\overrightarrow {AD} + \overrightarrow {CF} + \overrightarrow {EB} \);
D. \(\overrightarrow {AE} + \overrightarrow {BC} + \overrightarrow {DF} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 48
A. 10 cm;
B. 5 cm;
C. 11 cm;
D. 7 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 49
A. \(\overrightarrow {AB} = \overrightarrow {AC} ,\overrightarrow {OB} = \overrightarrow {AO} \);
B. \(\overrightarrow {AB} = \overrightarrow {OC} ;\overrightarrow {OB} = \overrightarrow {DO} \);
C. \(\overrightarrow {AB} = \overrightarrow {DC} ;\overrightarrow {OB} = \overrightarrow {AO} \);
D. \(\overrightarrow {AB} = \overrightarrow {DC} ;\overrightarrow {OB} = \overrightarrow {DO} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
A. 3 cm;
B. 4 cm;
C. 5 cm;
D. 6 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
A. \(\left( { - \infty ; - 5} \right) \cup \left[ {3; + \infty } \right)\);
B. \(\left( {5; + \infty } \right)\);
C. \(\left[ {3; + \infty } \right)\);
D. \(\left( { - \infty ; - 5} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.