Một nhóm 10 học sinh gồm 5 học sinh nam trong đó có An và 5 học sinh nữ trong đó có Bình được xếp ngồi vào 10 cái ghế trên một hàng ngang. Hỏi có bao nhiêu cách sắp xếp nam và nữ ngồi xen kẽ, đồng thời An không ngồi cạnh Bình?
Một nhóm 10 học sinh gồm 5 học sinh nam trong đó có An và 5 học sinh nữ trong đó có Bình được xếp ngồi vào 10 cái ghế trên một hàng ngang. Hỏi có bao nhiêu cách sắp xếp nam và nữ ngồi xen kẽ, đồng thời An không ngồi cạnh Bình?
A. 16.(4!)2;
B. 16.8!;
C. 32.(4!)2;
D. 32.8!.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: C
Xếp 10 học sinh sao có nam nữ ngồi xen kẽ.
Xếp 5 học sinh nam có 5! cách, xếp 5 học sinh nữ vào 5 vị trí còn lại có 5! cách.
Đổi chỗ nam và nữ có 2 cách.
Suy ra có 2.(5!)2 cách xếp 10 học sinh sao có nam nữ ngồi xen kẽ.
* Xếp 8 học sinh không có An và Bình trước:
• TH1:
+ Học sinh nam đứng đầu hàng, có (4!)2 cách.
+ Xếp An và Bình vào 1 trong 9 vị trí gồm 7 vị trí giữa 2 học sinh liền kề nhau và 2 vị trí biên. Ứng với mỗi vị trí có 1 cách xếp An và Bình sao cho thỏa mãn yêu cầu, do đó có 9 cách xếp.
Vậy có 9.(4!)2 cách.
• TH2:
+ Học sinh nữ đứng đầu hàng, tương tự TH1 có 9.(4!)2 (cách).
Suy ra số cách xếp 10 học sinh xen kẽ mà An luôn cạnh Bình là 2.9.(4!)2 (cách).
Vậy số cách sắp xếp nam và nữ ngồi xen kẽ, đồng thời An không ngồi cạnh Bình là:
2.(5!)2 – 2.9.(4!)2 = 2.5.5.(4!)2 – 18.(4!)2 = 32.(4!)2 (cách)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
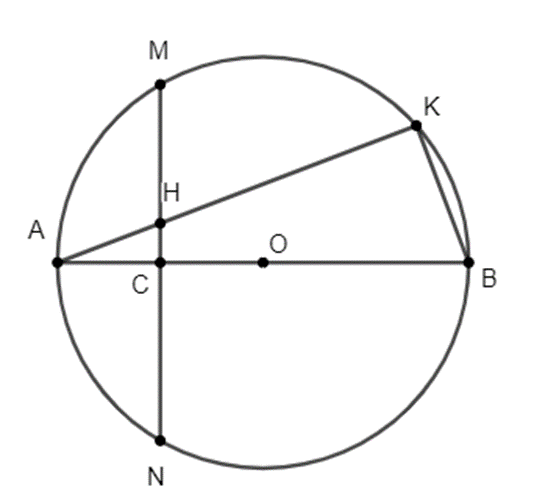
a) Ta có: \(\widehat {AKB} = 90^\circ \) (góc nội tiếp đường tròn (O)) \( \Rightarrow \widehat {HKB} = 90^\circ \).
Có: \(\widehat {ACH} = \widehat {HCB} = 90^\circ \) (MN\( \bot \)AB; H, C ∈ MN)
Xét tứ giác BCHK có \(\widehat {HCB} + \widehat {HKB} = 90^\circ + 90^\circ = 180^\circ \)
Suy ra tứ giác BCHK nội tiếp đường tròn.
b) Xét \(\Delta ACH\) và \(\Delta AKB\) có:
\(\widehat {BAK}\) chung
\(\widehat {ACH} = \widehat {AKB} = 90^\circ \) (cmt)
Suy ra \(\Delta AHC\) ᔕ \(\Delta AKB\)(g.g)
\( \Rightarrow \frac{{AH}}{{AB}} = \frac{{AC}}{{AK}}\)
\( \Leftrightarrow \)AH.AK = AC. AB \( = \frac{R}{2}.2R = {R^2}\) (đpcm)
Lời giải
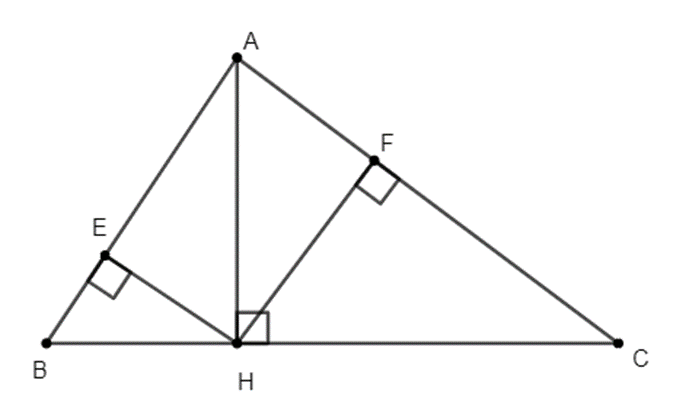
a) Áp dụng hệ thức lượng trong tam giác, ta có:
• Xét \(\Delta AHC\): AH2 = AF.AC
• Xét \(\Delta AHB\): AH2 = AE.AB
Do đó AE.AB = AF. AC
b) Ta có: AH2 = AE.AB
\( \Rightarrow AE = \frac{{A{H^2}}}{{AB}} = \frac{{{3^3}}}{4} = 2,25\) (cm)
Mà AE + BE = AB
\( \Rightarrow \)BE = AB – AE
= 4 – 2,24 = 1,75 (cm)
c) \(\Delta AHC\) vuông tại H
\( \Rightarrow \cos \widehat {HAC} = \frac{{AH}}{{AC}}\)
\(AC = \frac{6}{{\sqrt 3 }} = 2\sqrt 3 \) (cm)
Theo ý a) ta có: AE.AB = AF.AC
\( \Rightarrow AF = \frac{{AE.AB}}{{AC}} = \frac{{2,25.4}}{{2\sqrt 3 }} = \frac{{3\sqrt 3 }}{2}\)(cm)
FC = AC – AF
\( = 2\sqrt 3 - \frac{{3\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{2}\)(cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.