Cho tam giác ABC có trọng tâm G và tâm đường tròn ngoại tiếp O thỏa mãn \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \). Hỏi trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Vì sao?
1) \[\overrightarrow {OG} = \vec 0\].
2) Tam giác ABC là tam giác vuông cân.
3) Tam giác ABC là tam giác đều.
4) Tam giác ABC là tam giác cân.
Cho tam giác ABC có trọng tâm G và tâm đường tròn ngoại tiếp O thỏa mãn \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \). Hỏi trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Vì sao?
1) \[\overrightarrow {OG} = \vec 0\].
2) Tam giác ABC là tam giác vuông cân.
3) Tam giác ABC là tam giác đều.
4) Tam giác ABC là tam giác cân.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Xét tam giác ABC có G là trọng tâm. Theo tính chất của trọng tâm trong tam giác ta có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
\( \Rightarrow G \equiv O\).
Suy ra tam giác ABC có trọng tâm trùng với tâm của đường tròn ngoại tiếp là một tam giác đều.
• \[\overrightarrow {OG} = \overrightarrow {OO} = \overrightarrow 0 \] suy ra 1) đúng.
• 2) sai vì tam giác ABC là tam giác đều.
• 3), 4) đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
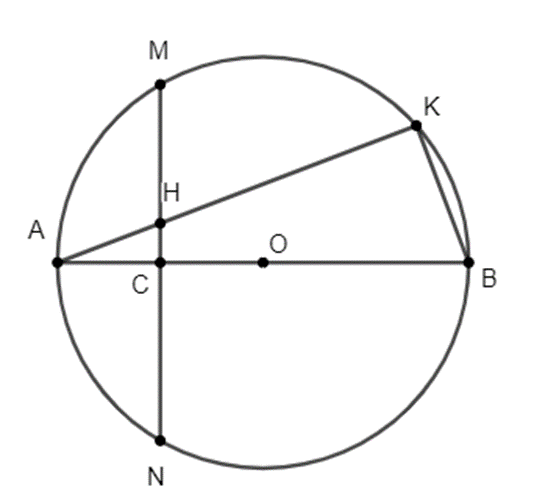
a) Ta có: \(\widehat {AKB} = 90^\circ \) (góc nội tiếp đường tròn (O)) \( \Rightarrow \widehat {HKB} = 90^\circ \).
Có: \(\widehat {ACH} = \widehat {HCB} = 90^\circ \) (MN\( \bot \)AB; H, C ∈ MN)
Xét tứ giác BCHK có \(\widehat {HCB} + \widehat {HKB} = 90^\circ + 90^\circ = 180^\circ \)
Suy ra tứ giác BCHK nội tiếp đường tròn.
b) Xét \(\Delta ACH\) và \(\Delta AKB\) có:
\(\widehat {BAK}\) chung
\(\widehat {ACH} = \widehat {AKB} = 90^\circ \) (cmt)
Suy ra \(\Delta AHC\) ᔕ \(\Delta AKB\)(g.g)
\( \Rightarrow \frac{{AH}}{{AB}} = \frac{{AC}}{{AK}}\)
\( \Leftrightarrow \)AH.AK = AC. AB \( = \frac{R}{2}.2R = {R^2}\) (đpcm)
Lời giải
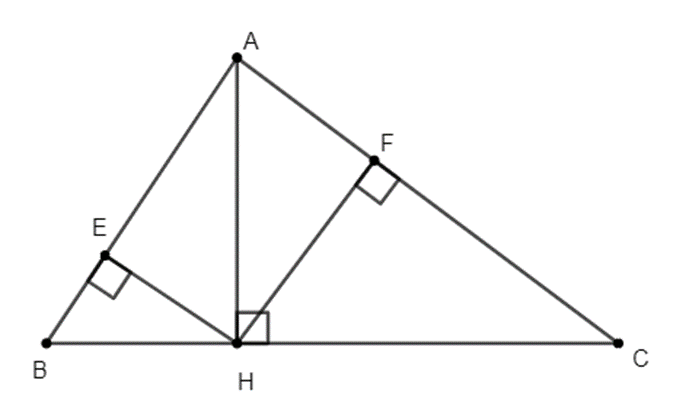
a) Áp dụng hệ thức lượng trong tam giác, ta có:
• Xét \(\Delta AHC\): AH2 = AF.AC
• Xét \(\Delta AHB\): AH2 = AE.AB
Do đó AE.AB = AF. AC
b) Ta có: AH2 = AE.AB
\( \Rightarrow AE = \frac{{A{H^2}}}{{AB}} = \frac{{{3^3}}}{4} = 2,25\) (cm)
Mà AE + BE = AB
\( \Rightarrow \)BE = AB – AE
= 4 – 2,24 = 1,75 (cm)
c) \(\Delta AHC\) vuông tại H
\( \Rightarrow \cos \widehat {HAC} = \frac{{AH}}{{AC}}\)
\(AC = \frac{6}{{\sqrt 3 }} = 2\sqrt 3 \) (cm)
Theo ý a) ta có: AE.AB = AF.AC
\( \Rightarrow AF = \frac{{AE.AB}}{{AC}} = \frac{{2,25.4}}{{2\sqrt 3 }} = \frac{{3\sqrt 3 }}{2}\)(cm)
FC = AC – AF
\( = 2\sqrt 3 - \frac{{3\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{2}\)(cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.