5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 29)
28 người thi tuần này 4.6 105.9 K lượt thi 45 câu hỏi 50 phút
- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Ta có:
Vậy \(\overrightarrow {AB} + \overrightarrow {C{\rm{D}}} = \overrightarrow {A{\rm{D}}} + \overrightarrow {CB} \).
Câu 2
Cho hàm số f(x) có đạo hàm f’(x) = x(x − 1)(x + 4)3 , ∀ x ∈ R. Số điểm cực tiểu của hàm số đã cho là
Cho hàm số f(x) có đạo hàm f’(x) = x(x − 1)(x + 4)3 , ∀ x ∈ R. Số điểm cực tiểu của hàm số đã cho là
A. 2;
B. 3;
C. 4;
D. 1.
Lời giải
Đáp án đúng là: A
Ta có
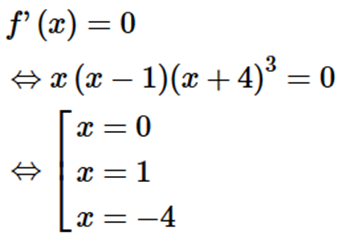
Ta có bảng xét dấu của f’(x)

Dựa vào bảng xét dấu của f'(x) suy ra hàm số đã cho có 2 điểm cực tiểu.
Vậy ta chọn đáp án A.
Câu 3
A. 2;
B. 0;
C. 1;
D. 3.
Lời giải
Đáp án đúng là C
Ta có:
f’(x) = 0 ⇔ x(x − 1)2 = 0 ⇔ \(\left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)
Ta xét dấu của f’ (x)

Ta thấy đạo hàm đổi dấu đúng 1 lần nên hàm số đã cho có đúng 1 cực trị
Vậy ta chọn đáp án C.
Lời giải
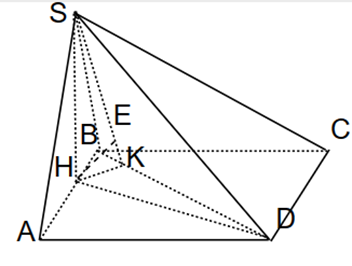
Gọi H là trung điểm của AB
Suy ra SH ⊥ (ACBD)
Do đó SH ⊥ HD
Hay tam giác SHD vuông tại H
Suy ra \(SH = \sqrt {S{{\rm{D}}^2} - D{H^2}} \)
Vì tam giác AHD vuông tại A
Nên \(D{H^2} = A{H^2} + A{{\rm{D}}^2} = \frac{{{a^2}}}{4} + {a^2} = \frac{5}{4}{a^2}\)
Suy ra \(SH = \sqrt {S{{\rm{D}}^2} - D{H^2}} = \sqrt {\frac{9}{4}{a^2} - \frac{5}{4}{a^2}} = \sqrt {{a^2}} = a\)
Ta có \({V_{S.ABC{\rm{D}}}} = \frac{1}{3}.SH.{S_{ABC{\rm{D}}}} = \frac{1}{3}.a.{a^2} = \frac{{{a^3}}}{3}\)
Gọi K là hình chiếu vuông góc của H trên BD và E là hình chiếu vuông góc của H trên SK
Ta có
\(\left\{ \begin{array}{l}B{\rm{D}} \bot HK\\B{\rm{D}} \bot SH\end{array} \right. \Rightarrow BH \bot (SHK)\)
Suy ra BD ⊥ HE
Mà SK ⊥ HE nên HE ⊥ (SBD)
Ta có: HK = HB . sin \(\widehat {KBH}\) = \(\frac{a}{2}.\sin 45^\circ = \frac{a}{2}.\frac{{\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{4}\)
Suy ra \(HE = \frac{{HS.HK}}{{\sqrt {H{{\rm{S}}^2} + H{K^2}} }} = \frac{{a.\frac{{a\sqrt 2 }}{4}}}{{\sqrt {{a^2} + \frac{{2{{\rm{a}}^2}}}{{16}}} }} = \frac{{{a^2}\sqrt 2 }}{{4\sqrt {\frac{9}{8}{a^2}} }} = \frac{a}{3}\)
Do đó d(A,(SBD) = 2 d(H,(SBD)) = 2 HE = \(\frac{{2{\rm{a}}}}{3}\)
Lời giải
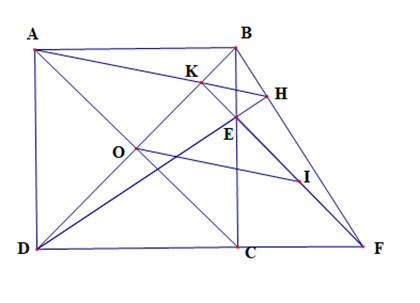
a) Vì ABCD là hình vuông nên AB = BC = CD = DA và
\(\widehat {ABC} = \widehat {BC{\rm{D}}} = \widehat {C{\rm{D}}A} = \widehat {DAB} = 90^\circ \)
Xét △DEC và △BFC có
EC = FC (giả thiết)
\(\widehat {DCE} = \widehat {BCF} = 90^\circ \)
DC = BC (chứng minh trên)
Do đó △DEC = △BFC (c.g.c)
Suy ra DE = BF (2 cạnh tương ứng), \(\widehat {E{\rm{D}}C} = \widehat {FBC}\)
b) Xét △BEH và △DEC có
\(\widehat {BEH} = \widehat {DEC}\) (hai góc đối đỉnh)
\(\widehat {E{\rm{D}}C} = \widehat {FBC}\) (chứng minh câu a)
Suy ra (g.g)
Do đó \(\widehat {BHE} = \overrightarrow {DCE} \)
Mà \(\overrightarrow {DCE} = 90^\circ \) nên \(\widehat {BHE} = 90^\circ \)
Hay DE ⊥ BF
Suy ra \(\widehat {DHF} = 90^\circ \)
c) Xét tam giác BDF có
DE ⊥ BF
BC ⊥ DF
DE cắt BC tại E
Suy ra E là trực tâm tam giác BDF
Do đó FK ⊥ BD
Mà AO ⊥ BD
Suy ra AO // IK
Vì CE = CF nên tam giác CEF cân tại C
Mà CI là trung tuyến
Suy ra CI là đường cao
Hay CI ⊥ EF
Xét tứ giác OKIC có
\(\widehat {OKI} = \widehat {K{\rm{O}}C} = \widehat {CIK} = 90^\circ \)
Suy ra OKIC là hình chữ nhật
Do đó OC = KI
Mà OC = AO
Suy ra AO = KI
Xét tứ giác AOIK có AO // KI , AO = KI (chứng minh trên)
Suy ra AOIK là hình bình hành
d) Xét tứ giác ABHD có \(\widehat {BA{\rm{D}}} + \widehat {BHD} = 90^\circ + 90^\circ = 180^\circ \)
Suy ra tứ giác ABHD nội tiếp
Do đó \(\widehat {AHB} = \widehat {A{\rm{D}}B} = 45^\circ \)
Xét tứ giác DKHF có \(\widehat {{\rm{DKF}}} = \widehat {DHF} = 90^\circ \)
Suy ra tứ giác DKHF nội tiếp
Do đó \(\widehat {KHB} = \widehat {{\rm{FD}}B} = 45^\circ \)
Suy ra \(\widehat {AHB} = \overrightarrow {KHB} \)
Suy ra AH ≡ KH
Do đó A, H, K thẳng hàng
Vậy A, H, K thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. Đường tròn tâm G đường kính BC
B. Đường tròn tâm G đường kính \(\frac{1}{3}\)BC
C. Đường tròn tâm G bán kính \(\frac{1}{3}\)BC
D. Đường tròn tâm G bán kính 3MG.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Cho hàm số f(x) có đạo hàm f’(x) = x(x – 1)(x + 2)3 ; ∀ x ∈ R. Số điểm cực trị của hàm số đã cho là:
Cho hàm số f(x) có đạo hàm f’(x) = x(x – 1)(x + 2)3 ; ∀ x ∈ R. Số điểm cực trị của hàm số đã cho là:
A. 3
B. 2
C. 5
D. 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. 0,26 . 10-3
B. 0,52 . 10-3
C. 0,37 . 10-3
D. 0,41 . 10-3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. (– ∞; 1) ∪ (1; + ∞);
B. (– ∞; 1) và (1; + ∞);
C. R ∖ {1};
D. (– ∞; + ∞).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 37
A. \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HH'} \)
B. \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HK} \)
C. \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow 0 \)
D. \(\overrightarrow {HM} + \overrightarrow {HN} + \overrightarrow {HP} = \overrightarrow {H'K} \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
A. y = f(x) = \(\sqrt 3 \)x2 + x – 4;
B. y = f(x) = x2 + \(\frac{1}{x}\) – 5;
C. y = f(x) = – 2x(x – 1);
D. y = f(x) = 2(x2 + 1) + 3x – 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.