Câu hỏi:
13/07/2024 1,059
Cho hình vuông ABCD, gọi O là tâm của hình vuông. Một đường thẳng qua O cắt AD tại P, cắt BC tại Q.
a) Chứng minh AP = CQ
b) Kẻ Px vuông góc AC tại E (E thuộc AC). Kẻ Qy vuông góc BD tại F (F thuộc BD), Px và Qy cắt nhau tại M. Chứng minh OEMF là hình chữ nhật.
c) Chứng minh M thuộc cạnh AB
d) Lấy K thuộc BC sao cho CK = DP. Chứng minh \(\widehat {MOK} = 90^\circ \).
Cho hình vuông ABCD, gọi O là tâm của hình vuông. Một đường thẳng qua O cắt AD tại P, cắt BC tại Q.
a) Chứng minh AP = CQ
b) Kẻ Px vuông góc AC tại E (E thuộc AC). Kẻ Qy vuông góc BD tại F (F thuộc BD), Px và Qy cắt nhau tại M. Chứng minh OEMF là hình chữ nhật.
c) Chứng minh M thuộc cạnh AB
d) Lấy K thuộc BC sao cho CK = DP. Chứng minh \(\widehat {MOK} = 90^\circ \).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
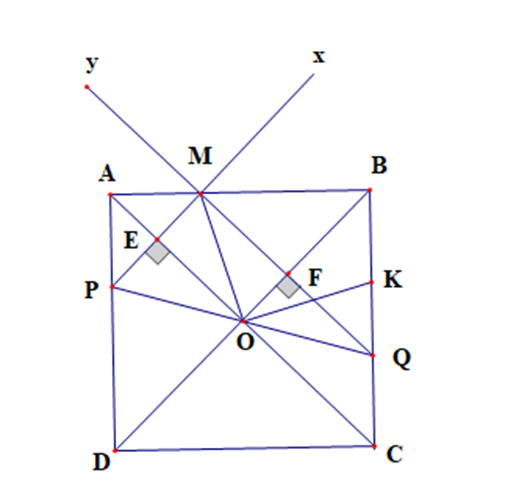
a) Vì ABCD là hình vuông tâm O
Nên OA = OB = OC = OD, AB = BC = CD = DA, AD // BC
Suy ra \(\widehat {DAC} = \widehat {ACB}\) (hai góc so le trong)
Xét tam giác AOP và tam gíc COQ có
\(\widehat {DAC} = \widehat {ACB}\) (chứng minh trên)
OA = OC (chứng minh trên)
\(\widehat {AOP} = \widehat {COQ}\) (hai góc đối đỉnh)
Do đó ΔAOP = ΔCOQ (g.c.g)
Suy ra AP = CQ (hai cạnh tương ứng)
b) Vì AB = AD nên tam giác ABD cân tại A
Mà AO là đường trung tuyến
Suy ra AO là đường cao
Hay AO ⊥ BD
Xét tứ giác OEMF có
\(\widehat {OEM} = \widehat {EOF} = \widehat {OFM} = 90^\circ \)
Suy ra OEMF là hình chữ nhật
c) Vì OEMF là hình chữ nhật
Nên \[\widehat {FME} = 90^\circ \]
Hay tam giác PMQ vuông tại M
Mà MO là trung tuyến
Suy ra OM = OP = OQ
Do đó tam giác POM cân tại O
Lại có OE là đường cao nên OE là phân giác của \(\widehat {POM}\)
Suy ra \(\widehat {POE} = \widehat {EOM}\)
Xét tam giác AOP và tam giác AOM có
AO là cạnh chung
\(\widehat {POE} = \widehat {EOM}\) (chứng minh trên)
OM = OP (chứng minh trên)
Suy ra △AOP = △AOM (c.g.c)
Do đó \(\widehat {AP{\rm{O}}} = \widehat {AM{\rm{O}}}\) (hai góc tương ứng)
Ta có OM = OQ
Do đó tam giác QOM cân tại O
Lại có OF là đường cao nên OF là phân giác của \(\widehat {QOM}\)
Suy ra \(\widehat {QOF} = \widehat {FOM}\)
Xét tam giác BOQ và tam giác BOM có
BO là cạnh chung
\(\widehat {QOF} = \widehat {FOM}\) (chứng minh trên)
OM = OQ (chứng minh trên)
Suy ra △ BOQ = △BOM (c.g.c)
Do đó \(\widehat {{\rm{BQO}}} = \widehat {BM{\rm{O}}}\) (hai góc tương ứng)
Vì AD // BC nên \(\widehat {AP{\rm{O}}} + \widehat {BQO} = 180^\circ \)
Mà \(\widehat {{\rm{BQO}}} = \widehat {BM{\rm{O}}}\), \(\widehat {AP{\rm{O}}} = \widehat {AM{\rm{O}}}\)
Suy ra \(\widehat {AM{\rm{O}}} + \widehat {BMO} = 180^\circ \)
Hay \(\widehat {AMB} = 180^\circ \)
Do đó A, M, B thẳng hàng
Vậy M thuộc cạnh AB
d) Ta có: AP = AD – DP, BK = BC – CK
Mà AD = BC, PD = CK
Suy ra AP = BK
Vì ABCD là hình vuông tâm O
Nên \(\widehat {DAO} = \widehat {OBC} = 45^\circ \)
Xét tam giác POA và tam giác KOB có
OA = OB
\(\widehat {DAO} = \widehat {OBC}\) (chứng minh trên)
PA = BK (chứng minh trên)
Suy ra △POA = △KOB (c.g.c)
Do đó \(\widehat {POA} = \widehat {K{\rm{OB}}}\) (hai góc tương ứng)
Mà \(\widehat {POA} = \widehat {{\rm{AOM}}}\)
Nên \(\widehat {KOB} = \widehat {{\rm{AOM}}}\)
Mặt khác \(\widehat {AOM} + \widehat {{\rm{MOB}}} = \widehat {AOB} = 90^\circ \) (hai góc kề bù)
Suy ra \(\widehat {BOK} + \widehat {{\rm{MOB}}} = 90^\circ \)
Hay \(\widehat {MOK} = 90^\circ \)
Vậy \(\widehat {MOK} = 90^\circ \).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Hàm số f(x) luôn xác định trên R
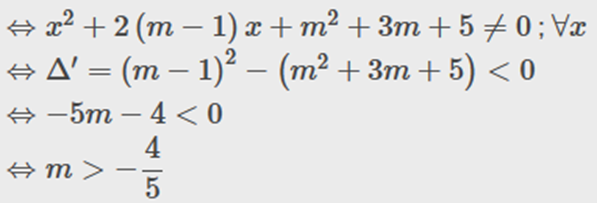
Vậy m > \(\frac{{ - 4}}{5}\).
b) Hàm số f(x) luôn xác định trên R
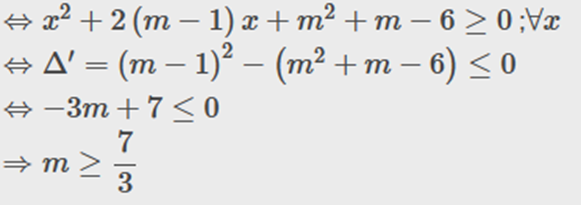
Vậy m ≥ \(\frac{7}{3}\).
c) ) Hàm số f(x) luôn xác định trên R
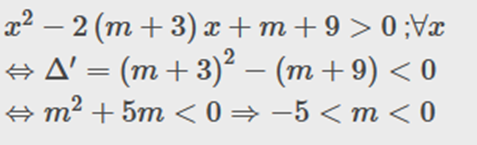
Vậy – 5 < m < 0.
Lời giải
Ta có :
\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {CF} + \overrightarrow {FD} + \overrightarrow {EB} + \overrightarrow {BF} \)
\( = (\overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} ) + (\overrightarrow {FD} + \overrightarrow {DB} + \overrightarrow {BF} ) = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} + \overrightarrow {FF} \)
\( = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} + \overrightarrow 0 = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \)
Vậy \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận